Hint - You will get a Lie derivative along the way.
\[ \boldsymbol{\sigma} = {1 \over J} \, {\bf F} \cdot \boldsymbol{\sigma}^\text{PK2} \cdot {\bf F}^T \]
Take the time derivative
\[ \dot{\boldsymbol{\sigma}} = - \left( {\dot J \over J^2} \right) \, {\bf F} \cdot \boldsymbol{\sigma}^\text{PK2} \cdot {\bf F}^T + {1 \over J} \, \dot{\bf F} \cdot \boldsymbol{\sigma}^\text{PK2} \cdot {\bf F}^T + {1 \over J} \, {\bf F} \cdot \dot {\boldsymbol{\sigma}}^\text{PK2} \cdot {\bf F}^T + {1 \over J} \, {\bf F} \cdot \boldsymbol{\sigma}^\text{PK2} \cdot \dot{\bf F}^T \]
And substitute in several identities
\[ \text{tr}({\bf D}) = {\dot J \over J} \quad \qquad \dot{\bf F} = {\bf L} \cdot {\bf F} \qquad \quad \dot{\bf F}^T = {\bf F}^T \cdot {\bf L}^T \]
to get
\[ \dot{\boldsymbol{\sigma}} = - \text{tr}({\bf D}) {1 \over J} {\bf F} \cdot {\boldsymbol{\sigma}}^\text{PK2} \cdot {\bf F}^T + {1 \over J} \, {\bf L} \cdot {\bf F} \cdot {\boldsymbol{\sigma}}^\text{PK2} \cdot {\bf F}^T + {1 \over J} \, {\bf F} \cdot \dot{\boldsymbol{\sigma}}^\text{PK2} \cdot {\bf F}^T + {1 \over J} \, {\bf F} \cdot {\boldsymbol{\sigma}}^\text{PK2} \cdot {\bf F}^T \cdot {\bf L}^T \]
This big equation can be shortened by recognizing that many of the terms contain \({1 \over J} \, {\bf F} \cdot{\boldsymbol{\sigma}}^\text{PK2} \cdot {\bf F}^T\), which is just the Cauchy stress, \(\boldsymbol{\sigma}\).
\[ \dot{\boldsymbol{\sigma}} = - \text{tr}({\bf D}) \; \boldsymbol{\sigma} + {\bf L} \cdot \boldsymbol{\sigma} + \boldsymbol{\sigma} \cdot {\bf L}^T + {1 \over J} \, {\bf F} \cdot \dot{\boldsymbol{\sigma}}^\text{PK2} \cdot {\bf F}^T \]
This is the relationship between the time derivative of the 2nd Piola-Kirchhoff stress, \(\dot{\boldsymbol{\sigma}}^\text{PK2}\), and the Cauchy stress, \(\dot{\boldsymbol{\sigma}}\).
After a little rearrangement...
\[ \dot{\boldsymbol{\sigma}} - {\bf L} \cdot \boldsymbol{\sigma} - \boldsymbol{\sigma} \cdot {\bf L}^T = - \text{tr}({\bf D}) \; \boldsymbol{\sigma} + {1 \over J} \, {\bf F} \cdot \dot{\boldsymbol{\sigma}}^\text{PK2} \cdot {\bf F}^T \]
And the left hand side is the Lie derivative, so the equation can be written more compactly as
\[ {\buildrel \nabla \over {\boldsymbol{\sigma}}} = - \text{tr}({\bf D}) \; \boldsymbol{\sigma} + {1 \over J} \, {\bf F} \cdot \dot{\boldsymbol{\sigma}}^\text{PK2} \cdot {\bf F}^T \]
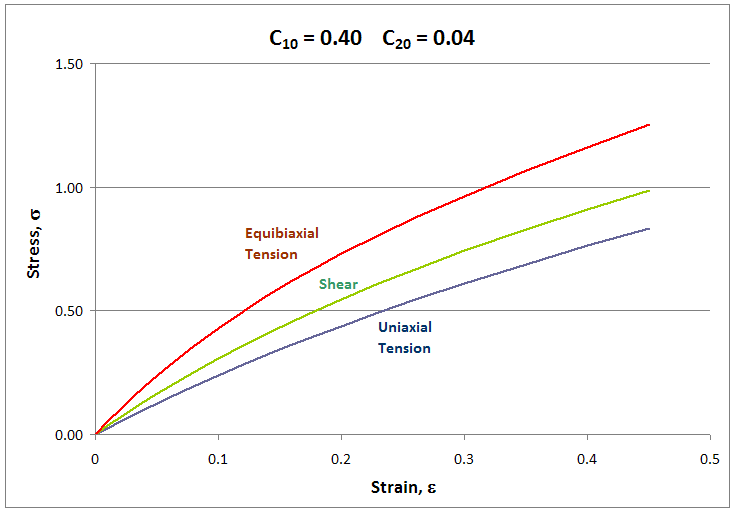
\[ W = C_{10} \left( I_1 - 3 \right) \]
and show how to get to the following equation for uniaxial tension.
\[ \sigma^\text{Eng} = 2 \, C_{10} \left( \lambda - {1 \over \lambda^2 } \right) \]
\[ W = C_{10} \left( \lambda_1^2 + \lambda_2^2 + \lambda_3^2 - 3 \right) \]
Substitute
\[ \lambda_3 = {1 \over \lambda_1 \lambda_2} \]
Substitute
\[ W = C_{10} \left( \lambda_1^2 + \lambda_2^2 + {1 \over \lambda_1^2 \lambda_2^2} - 3 \right) \]
Take the derivative with respect to \(\lambda_1\).
\[ \sigma^\text{Eng} = {\partial W \over \partial \lambda_1} = 2 \, C_{10} \left( \lambda_1 - {1 \over \lambda_1^3 \lambda_2^2} \right) \]
For uniaxial tension, substitute \(\lambda_2 = 1 / \sqrt{\lambda_1}\) to get
\[ \sigma^\text{Eng} = 2 \, C_{10} \left( \lambda_1 - {1 \over \lambda_1^2 } \right) \]
Yes, this question is basically the same as #1 above, but with Mooney-Rivlin terms instead.