(a) all three transformed axes are the same angle from the Z axis, and
(b) the new x' axis is directly above the X axis (no Y component).
The z-components satisfy \(z_1^2 + z_2^2 + z_3^3 = 1\). But since \(z_1 = z_2 = z_3\), this becomes \(3 z^2 = 1\). So \(z_1 = z_2 = z_3 = \sqrt{1/3} = 0.5774\).
The \({\bf i'}\) vector has no y-component, so \(x_1^2 + z_1^2 = 1\). This gives \(x_1 = \sqrt{2/3} = 0.8165\).
For \({\bf j'}\), \(x_2^2 + y_2^2 + z_2^2 = 1\). And since \({\bf k'}\) can be written in terms of \({\bf j'}\) components as \((x_2, -y_2, z_2)\). So \({\bf j'} \cdot {\bf k'} = x_2^2 - y_2^2 + z_2^2 = 0\). Subtracting the two equations gives \(2 y_2^2 = 1\), so \(y_2 = \sqrt{1/2} = 0.7071\), and that leaves \(x_2 = \sqrt{1/6} = 0.4082\). So
\[ {\bf Q} = \left[ \matrix{ \;\;\;0.8165 & \;\;\;0.0000 & 0.5774 \\ -0.4082 & \;\;\;0.7071 & 0.5774 \\ -0.4082 & -0.7071 & 0.5774 } \right] \]
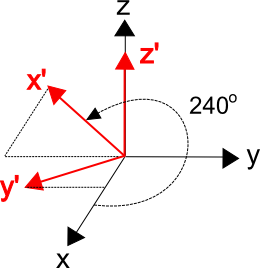
\[ \psi = \text{Tan}^{-1}(q_{32}/q_{31}) = \text{Tan}^{-1}(-0.7071 / -0.4082) = 240^\circ \]
\[ \theta = \text{Cos}^{-1}(q_{33}) = \text{Cos}^{-1}(0.5774) = 54.73^\circ \]
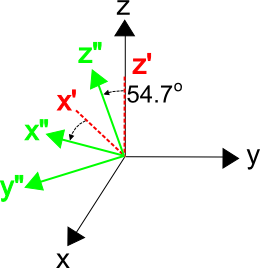
\[ \phi = \text{Tan}^{-1}(q_{23}/-q_{13}) = \text{Tan}^{-1}(0.5774 / -0.5774) = 135^\circ \]
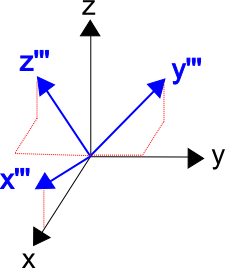
\[ \alpha = \text{Cos}^{-1} \left\{ {1\over 2} \Big[ \text{tr}({\bf Q}) - 1 \Big] \right\} = 56.6^\circ \]
\[ p_1 = { q_{23} - q_{32} \over 2 \sin \alpha } = {0.5774 - (-0.7071) \over 2 \sin(56.6^\circ)} = 0.7693 \]
\[ p_2 = { q_{31} - q_{13} \over 2 \sin \alpha } = {-0.4082 - 0.5774 \over 2 \sin(56.6^\circ)} = -0.5903 \]
\[ p_3 = { q_{12} - q_{21} \over 2 \sin \alpha } = {0.0000 - (-0.4082) \over 2 \sin(56.6^\circ)} = 0.2445 \]
After 180° rotation, \( {\bf v'} = (-5,-9) \) and \({\bf A'} = \left[ \matrix { 5 & 2 \\ 2 & 3 } \right] \). So \({\bf v'} = -{\bf v}\) and \({\bf A'} = {\bf A}\).
\[ \begin{eqnarray} \nabla \cdot \nabla || {\bf x} || & = & \nabla^2 || {\bf x} || \\ \\ & = & \left[ (x_i x_i)^{1 \over 2} \right]_{,jj} \\ \\ & = & \left[ {1 \over 2 } (x_i x_i)^{-{1 \over 2}} (x_i x_{i,j} + x_{i,j} x_i) \right]_{,j} \\ \\ & = & \left[ {1 \over 2 } (x_i x_i)^{-{1 \over 2}} (x_k x_{k,j} + x_{k,j} x_k) \right]_{,j} \\ \\ & = & \left[ {1 \over 2 } (x_i x_i)^{-{1 \over 2}} (x_k \delta_{kj} + \delta_{kj} x_k) \right]_{,j} \\ \\ & = & \left[ {1 \over 2 } (x_i x_i)^{-{1 \over 2}} (x_j + x_j) \right]_{,j} \\ \\ & = & \left[ (x_i x_i)^{-{1 \over 2}} x_j \right]_{,j} \\ \\ & = & (x_i x_i)^{-{1 \over 2}} x_{j,j} - {1 \over 2 } x_j (x_i x_i)^{-{3 \over 2}} (x_i x_{i,j} + x_{i,j} x_i) \\ \\ & = & (x_i x_i)^{-{1 \over 2}} x_{j,j} - {1 \over 2 } x_j (x_i x_i)^{-{3 \over 2}} (x_k x_{k,j} + x_{k,j} x_k) \\ \\ & = & (x_i x_i)^{-{1 \over 2}} \delta_{jj} - {1 \over 2 } x_j (x_i x_i)^{-{3 \over 2}} (x_k \delta_{kj} + \delta_{kj} x_k) \\ \\ & = & 3 (x_i x_i)^{-{1 \over 2}} - {1 \over 2 } x_j (x_i x_i)^{-{3 \over 2}} (2 x_j ) \\ \\ & = & 3 (x_i x_i)^{-{1 \over 2}} - x_j (x_i x_i)^{-{3 \over 2}} x_j \\ \\ & = & 3 (x_i x_i)^{-{1 \over 2}} - (x_i x_i)^{-{3 \over 2}} (x_j x_j) \\ \\ & = & 3 (x_i x_i)^{-{1 \over 2}} - (x_i x_i)^{-{1 \over 2}} \\ \\ & = & 2 (x_i x_i)^{-{1 \over 2}} \\ \\ & = & 2 / || {\bf x} || \end{eqnarray} \]