\[ \epsilon_{ijk} \, \epsilon_{ijk} = 6 \]
Use the epsilon-delta identity.
\[ \begin{eqnarray} \epsilon_{ijk} \, \epsilon_{ijk} & = & \delta_{jj} \delta_{kk} - \delta_{jk} \delta_{jk} \\ \\ \\ & = & 3 * 3 - \delta_{kk} \\ \\ \\ & = & 9 - 3 \\ \\ \\ & = & 6 \end{eqnarray} \]
\[ \boldsymbol{\sigma} = \left[ \matrix{ 10 & 20 & 30 \\ 20 & 40 & 50 \\ 30 & 50 & 60 } \right] \qquad \]
One of the two stress tensors below is equivalent to the one above, differing only by a coordinate transformation. The other one represents a different stress state. Which is equivalent and which is different?
\[ \left[ \matrix{ 4.0341 & 27.291 & 14.519 \\ 27.291 & 76.619 & 46.048 \\ 14.519 & 46.048 & 29.347 } \right] \qquad \qquad \qquad \left[ \matrix{ \;\;\;30.597 & -5.733 & -15.201 \\ \;-5.733 & \;41.305 & \;\;\;18.926 \\ -15.201 & \;18.926 & \;\;\;48.098 } \right] \]
The way to tackle this question is to compare principal stresses.
The principal values of the given stress tensor are
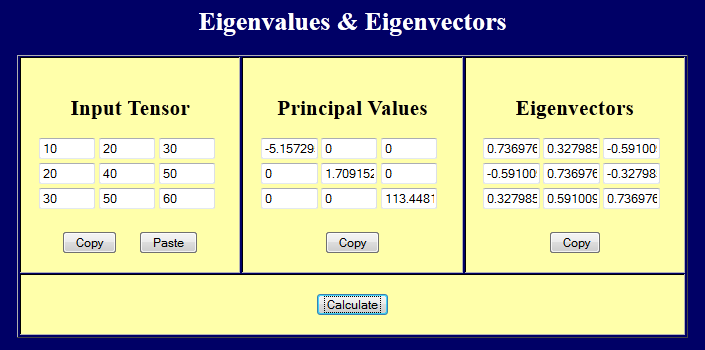
The principal values of the 1st candidate tensor are
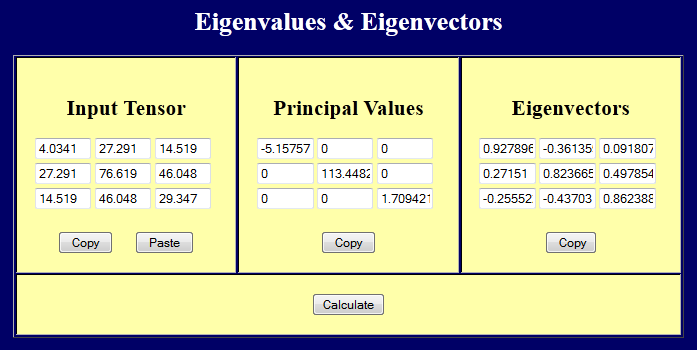
The above image shows that it is this first candidate stress tensor that is equivalent to the given stress tensor. The fact that the principal values are in a different order only means that the software found principal orientations for the two tensors that are 90° apart. This is nothing but a coordinate transformation.
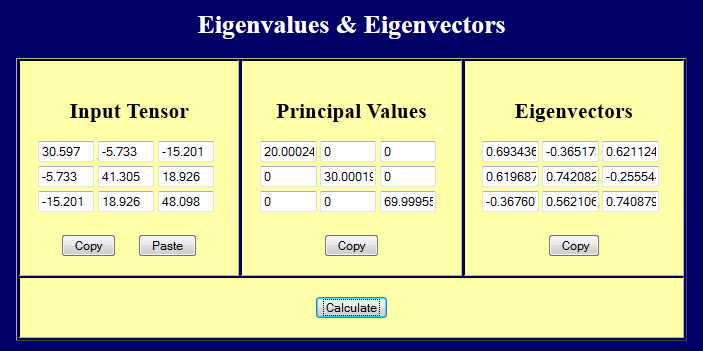
The principal values of the 2nd candidate stress tensor are: 20, 30, 70. Therefore, this 2nd candidate is not equivalent to the original stress tensor.
Calculate \(C_{1111}\), \(C_{1122}\), and \(C_{1133}\) and use them with the strains to calculate \(\sigma_{11}\).
It should simply equal \(\sigma_{11} = 1 \, \text{MPa}\) because this satisfies \(\sigma_{11} = E \epsilon_{11}\) for this case of uniaxial tension.
Start with the the equation for \(C_{ijkl}\).
\[ C_{ijkl} = {E \over (1 + \nu)} \left[ {1 \over 2} ( \delta_{ik} \, \delta_{jl} + \delta_{jk} \, \delta_{il} ) + { \nu \over (1 - 2 \nu)} \delta_{ij} \, \delta_{kl} \right] \]
and insert values for \(E\), \(\nu\), and the subscripts to get
\[ \begin{eqnarray} C_{1111} & = & {E \over (1 + \nu)} \left[ {1 \over 2} ( \delta_{11} \, \delta_{11} + \delta_{11} \, \delta_{11} ) + { \nu \over (1 - 2 \nu)} \delta_{11} \, \delta_{11} \right] \\ \\ \\ & = & {E \over (1 + \nu)} \left[ 1 + { \nu \over (1 - 2 \nu)} \right] \\ \\ \\ & = & {E \, ( 1 - \nu) \over (1 + \nu) (1 - 2 \nu) } \\ \\ \\ & = & {10 \, ( 1 - 0.333) \over (1 + 0.333) (1 - 2 * 0.333) } \\ \\ \\ \\ & = & 14.981 \, \text {MPa} \end{eqnarray} \]
\[ \begin{eqnarray} C_{1122} = C_{1133} & = & {E \over (1 + \nu)} \left[ {1 \over 2} ( \delta_{12} \, \delta_{12} + \delta_{12} \, \delta_{12} ) + { \nu \over (1 - 2 \nu)} \delta_{11} \, \delta_{22} \right] \\ \\ \\ & = & {E \, \nu \over (1 + \nu) (1 - 2 \nu) } \\ \\ \\ & = & {10 \, ( 0.333) \over (1 + 0.333) (1 - 2 * 0.333) } \\ \\ \\ \\ & = & 7.491 \, \text {MPa} \end{eqnarray} \]
and since all strain components are zero except \(\epsilon_{11}\), \(\epsilon_{22}\), and \(\epsilon_{33}\)
\[ \begin{eqnarray} \sigma_{11} & = & C_{1111} \, \epsilon_{11} + C_{1122} \, \epsilon_{22} + C_{1133} \, \epsilon_{33} \\ \\ \\ & = & ( 14.981 \, \text{MPa} ) ( 0.100 ) + ( 7.491 \, \text{MPa} ) ( -0.0333 ) + ( 7.491 \, \text{MPa} ) ( -0.0333 ) \\ \\ \\ & = & 1.00 \, \text{MPa} \end{eqnarray} \]