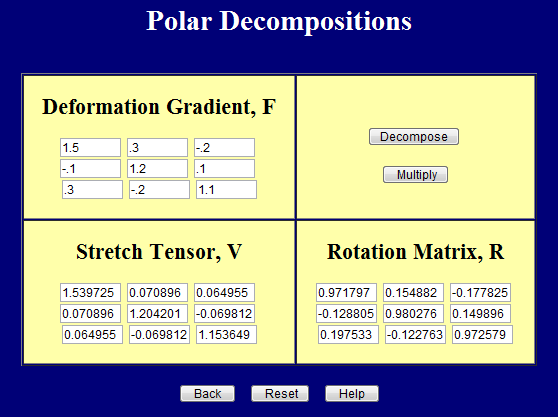
Do it the hard way by multiplying all the matrices out yourself (but not by hand! use software).
Then check your result using this page: http://www.continuummechanics.org/cm/techforms/RUDecomposition.html
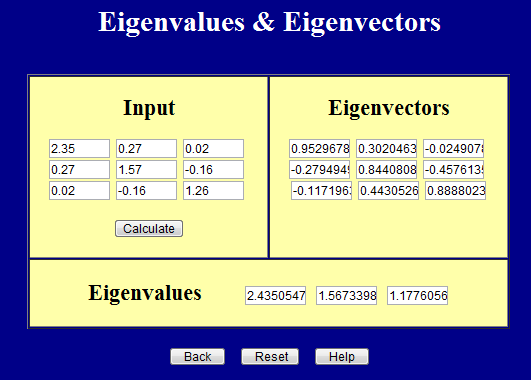
\[ {\bf F}^T \cdot {\bf F} = \left[ \matrix{ 2.35 & \;\;\;0.27 & \;\;\;0.02 \\ 0.27 & \;\;\;1.57 & -0.16 \\ 0.02 & -0.16 & \;\;\; 1.26 } \right] = {\bf U}^T \cdot {\bf U} \]
The principal values of \({\bf U}^T \cdot {\bf U}\) are
\[ ({\bf U}^T \cdot {\bf U})' = \left[ \matrix{ 2.4351 & 0 & 0 \\ 0 & 1.5673 & 0 \\ 0 & 0 & 1.1776 } \right] \]
and the transformation matrix is
\[ {\bf Q} = \left[ \matrix{ \;\;\;0.9530 & 0.3020 & -0.0249 \\ -0.2795 & 0.8441 & -0.4576 \\ -0.1172 & 0.4431 & \;\;\;0.8888 } \right] \]
Take the square root of \(({\bf U}^T \cdot {\bf U})'\) to get \({\bf U}'\).
\[ {\bf U}' = \left[ \matrix{ 1.5605 & 0 & 0 \\ 0 & 1.2519 & 0 \\ 0 & 0 & 1.0852 } \right] \]
And rotate \({\bf U}'\) back by using
\[ {\bf U} = {\bf Q}^T \cdot {\bf U}' \cdot {\bf Q} \]
\[ \begin{eqnarray} {\bf U} & = & \left[ \matrix{ \;\;\;0.9530 & -0.2795 & -0.1172 \\ \;\;\;0.3020 & \;\;\;0.8441 & \;\;\;0.4431 \\ -0.0249 & -0.4576 & \;\;\;0.8888 } \right] \left[ \matrix{ 1.5605 & 0 & 0 \\ 0 & 1.2519 & 0 \\ 0 & 0 & 1.0852 } \right] \left[ \matrix{ \;\;\;0.9530 & 0.3020 & -0.0249 \\ -0.2795 & 0.8441 & -0.4576 \\ -0.1172 & 0.4431 & \;\;\;0.8888 } \right] \\ \\ \\ & = & \left[ \matrix{ 1.5295 & \;\;\;0.0973 & \;\;\;0.0101 \\ 0.0973 & \;\;\;1.2473 & -0.0679 \\ 0.0101 & -0.0679 & \;\;\;1.1291 } \right] \end{eqnarray} \]
The inverse of \({\bf U}\) is
\[ {\bf U}^{-1} = \left[ \matrix{ 0.6572 & -0.0518 & -0.0090 \\ -0.0517 & 0.8084 & 0.0491 \\ -0.0090 & 0.0491 & 0.8887 } \right] \]
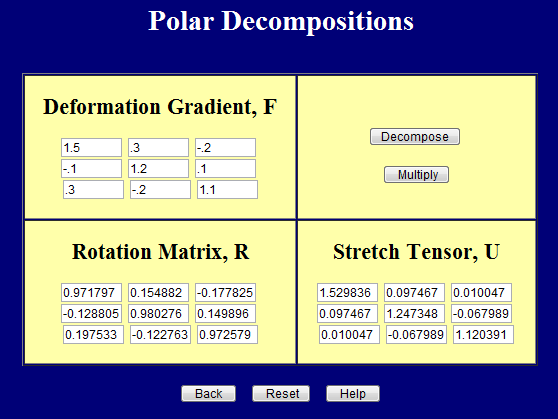
and the rotation matrix is
\[ \begin{eqnarray} {\bf R} & = & {\bf F} \cdot {\bf U}^{-1} & = & \left[ \matrix{ \;\;\; 1.5 & \;\;\; 0.3 & -0.2 \\ -0.1 & \;\;\;1.2 & \;\;\; 0.1 \\ \;\;\; 0.3 & -0.2 & \;\;\; 1.1 } \right] \left[ \matrix{ \;\;\;0.6572 & -0.0518 & -0.0090 \\ -0.0517 & \;\;\;0.8084 & \;\;\;0.0491 \\ -0.0090 & \;\;\;0.0491 & \;\;\;0.8887 } \right] \\ \\ & & & = & \left[ \matrix{ \;\;\;0.9721 & \;\;\;0.1550 & -0.1765 \\ -0.1287 & \;\;\;0.9802 & \;\;\;0.1487 \\ \;\;\;0.1976 & -0.1232 & \;\;\;0.9651 } \right] \end{eqnarray} \]
\[ \begin{eqnarray} \cos \alpha & = & \frac{1}{2} \left( \text{tr}({\bf R}) - 1 \right) \\ \\ \\ & = & \frac{1}{2} (0.9718 + 0.9803 + 0.9726 - 1) \\ \\ \\ \alpha & = & 15.8^\circ \end{eqnarray} \]
The unit vector for the axis of rotation is
\[ p_1 = { R_{32} - R_{23} \over 2 \sin \alpha } \qquad \qquad p_2 = { R_{13} - R_{31} \over 2 \sin \alpha } \qquad \qquad p_3 = { R_{21} - R_{12} \over 2 \sin \alpha } \]
Inserting values gives
\[ p_1 = { \text{-}0.1232 - 0.1487 \over 2 \sin 15.8^\circ } \qquad \qquad p_2 = { \text{-}0.1765 - 0.1976 \over 2 \sin 15.8^\circ } \qquad \qquad p_3 = { \text{-}0.1287 - 0.1550 \over 2 \sin 15.8^\circ } \]
The axis is
\[ {\bf p} = (-0.499, -0.687, -0.521) \]
\[ {\bf V} = {\bf R} \cdot {\bf U} \cdot {\bf R}^T \]
\[ \begin{eqnarray} {\bf V} & = & \left[ \matrix{ \;\;\;0.9718 & \;\;\;0.1549 & -0.1778 \\ -0.1288 & \;\;\;0.9803 & \;\;\;0.1499 \\ \;\;\;0.1975 & -0.1228 & \;\;\;0.9726 } \right] \left[ \matrix{ 1.5298 & \;\;\;0.0975 & \;\;\;0.0100 \\ 0.0975 & \;\;\;1.2473 & -0.0680 \\ 0.0100 & -0.0680 & \;\;\;1.1204 } \right] \left[ \matrix{ \;\;\;0.9718 & -0.1288 & \;\;\;0.1975 \\ \;\;\;0.1549 & \;\;\;0.9803 & -0.1228 \\ -0.1778 & \;\;\;0.1499 & \;\;\;0.9726 } \right] \\ \\ \\ & = & \left[ \matrix{ 1.5397 & \;\;\;0.0709 & \;\;\;0.0649 \\ 0.0709 & \;\;\;1.2042 & -0.0699 \\ 0.0649 & -0.0698 & \;\;\;1.1537 } \right] \end{eqnarray} \]