Introduction
A rotation matrix, \({\bf R}\), describes the rotation of an object in 3-D space. It was introduced on the previous two pages covering deformation gradients and polar decompositions.The rotation matrix is closely related to, though different from, coordinate system transformation matrices, \({\bf Q}\), discussed on this coordinate transformation page and on this transformation matrix page.
A transformation matrix describes the rotation of a coordinate system while an object remains fixed. In contrast, a rotation matrix describes the rotation of an object in a fixed coordinate system. The amazing fact, and often a confusing one, is that each matrix is the transpose of the other.
This entire page is essentially the transpose of the transformation matrix page. The two pages together border on being redundant. However, there are subtle differences between the two and they are stressed on this page.
Summary
The rotation matrix, \({\bf R}\), is used in the rotation of vectors and tensors while the coordinate system remains fixed. The vector or tensor is usually related to some object that is actually undergoing the rotation, and the vector and/or tensor is along for the ride.The general rules for applying the rotation matrix are the same as for the coordinate transformation matrix.
| Vectors | \({\bf v'}\) | \( = \) | \({\bf R} \cdot {\bf v}\) | |
| 2nd Rank Tensors | \(\boldsymbol{\sigma'}\) | \( = \) | \({\bf R} \cdot \boldsymbol{\sigma} \cdot {\bf R}^T\) | |
| 4th Rank Tensors | \({\bf C'}\) | \( = \) | \({\bf R} \cdot {\bf R} \cdot {\bf C} \cdot {\bf R}^T \cdot {\bf R}^T\) |
and in tensor notation...
| Vectors | \(v'_i\) | \( = \) | \(R_{ij} v_j\) | |
| 2nd Rank Tensors | \(\sigma'_{mn}\) | \( = \) | \(R_{mi} R_{nj} \sigma_{ij}\) | |
| 4th Rank Tensors | \(C'_{mnop}\) | \( = \) | \(R_{mi} R_{nj} R_{ok} R_{pl} C_{ijkl} \) |
In two dimensions, \({\bf R}\) is
\[ {\bf R} = \left[ \matrix {\cos \theta & -\sin \theta \\ \sin \theta & \;\;\;\cos \theta} \right] \]
where \(\theta\) is the rotation angle. Note that \({\bf R}\) is just the transpose of \({\bf Q}\), i.e., \({\bf R} = {\bf Q}^T\) and \({\bf Q} = {\bf R}^T\).
Rotation Matrix Properties
Rotation matrices have several special properties that, while easily seen in this discussion of 2-D vectors, are equally applicable to 3-D applications as well. This list is useful for checking the accuracy of a rotation matrix if questions arise. While a matrix still could be wrong even if it passes all these checks, it is definitely wrong if it fails even one!- The determinant of \({\bf R}\) equals one.
- The inverse of \({\bf R}\) is its transpose (this is discussed at the bottom of this page).
- The dot product of any row or column with itself equals one.
Ex: \( (\cos \theta \; {\bf i} + \sin \theta \; {\bf j}) \cdot (\cos \theta \; {\bf i} + \sin \theta \; {\bf j}) = 1 \)
- The dot product of any row with any other row equals zero.
Ex: \( (\cos \theta \; {\bf i} + \sin \theta \; {\bf j}) \cdot (-\sin \theta \; {\bf i} + \cos \theta \; {\bf j}) = 0 \)
- The dot product of any column with any other column equals zero.
Ex: \( (\cos \theta \; {\bf i} - \sin \theta \; {\bf j}) \cdot (\sin \theta \; {\bf i} + \cos \theta \; {\bf j}) = 0 \)
Multiplication of Rotation Matrices
Recall from above that the dot product of any two different rows or columns of a rotation matrix is zero, while the dot product of any row or column with itself is one. This can be written in matrix and tensor notation as\[ {\bf R} \cdot {\bf R}^T = {\bf I} \qquad \qquad \text{and} \qquad \qquad R_{ik} R_{jk} = \delta_{ij} \]
This shows that the transpose of a rotation matrix is also its inverse.
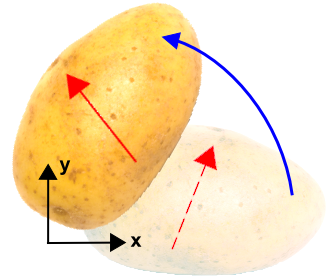
Rotating the Potato...
Recall that the vector on the potato was\[ {\bf v} = 2 {\bf \hat{i}} + 9 {\bf \hat{j}} \]
and the 50° counter-clockwise rotation of the coordinate system yielded
\[ {\bf v}' = 8.18 {\bf \hat{i}}' + 4.25 {\bf \hat{j}}' \]
In contrast, rotating the potato itself 50° counter clockwise gives
\[ \left\{ \matrix {v'_x \\ v'_y} \right\} = \left[ \matrix {\cos 50^\circ & -\sin 50^\circ \\ \sin 50^\circ & \;\;\;\cos 50^\circ} \right] \left\{ \matrix {2 \\ 9} \right\} \longrightarrow \left\{ \matrix {-5.609 \\ \;\;\;7.317 } \right\} \]
So the rotated vector is
\[ {\bf v}' = -5.609 {\bf \hat{i}} + 7.317 {\bf \hat{j}} \]
Note that the apostrophe is on \({\bf v}'\) to signify that it is somehow different from the reference \({\bf v}\) vector (rotated in this case), but it is not on \({\bf i}\) and \({\bf j}\) because they are still in the reference coordinate system.
Comparing Rotations to Transformations
The previous example rotated the potato and vector 50° counter-clockwise. This example will instead rotate the coordinate system 50° clockwise, so \(\theta\) will be -50° this time.\[ \left\{ \matrix {v'_x \\ v'_y} \right\} = \left[ \matrix {\;\;\;\cos (\text{-}50^\circ) & \sin (\text{-}50^\circ) \\ -\sin (\text{-}50^\circ) & \cos (\text{-}50^\circ)} \right] \left\{ \matrix {2 \\ 9} \right\} \longrightarrow \left\{ \matrix {-5.609 \\ \;\;\;7.317 } \right\} \]
So the vector can be written as
\[ {\bf v}' = -5.609 {\bf \hat{i}}' + 7.317 {\bf \hat{j}}' \]
in the rotated coordinate system. The important point to be made here is that the numerical values of the rotated vector in the 1st example and the vector in the oppositely-rotated coordinate system of this example, are the same.
\[ {\bf R} = \left[ \matrix { \cos(x',x) & \cos(y',x) & \cos(z',x) \\ \cos(x',y) & \cos(y',y) & \cos(z',y) \\ \cos(x',z) & \cos(y',z) & \cos(z',z) } \right] \]
where \((x',x)\) represents the angle between the \(x'\) and \(x\) axes, \((x',y)\) is the angle between the \(x'\) and \(y\) axes, etc. Yes, this is indeed the transpose of \({\bf Q}\).
3-D Reduction to 2-D
So a rotation about the \(z\)-axis means that \(\cos(z',z) = 1\) because the angle between \(z'\) and \(z\) remains 0°. Meanwhile, \(\cos(x',z) = \cos(y',z) = \cos(z',x) = \cos(z',y) = 0\) because the angles between these axes remains 90°.The angle between \(y'\) and \(x\) is \((90^\circ + \theta)\), and \(\cos(y',x) = \cos(90^\circ + \theta) = -\sin \theta\).
Likewise, the angle between \(x'\) and \(y\) is \((90^\circ - \theta)\), and \(\cos(x',y) = \cos(90^\circ - \theta) = \sin \theta\).
All of this leads to
\[ {\bf R} = \left[ \matrix { \cos \theta & -\sin \theta & 0 \\ \sin \theta & \;\;\;\cos \theta & 0 \\ 0 & 0 & 1 } \right] \]
which reveals the 2-D rotation matrix within the 3-D matrix.
An alternative way of interpreting and generating the rotation matrix is as follows.
\[ {\bf R} = \left[ \matrix { \left( \matrix{\text{x-comp} \\ \text{of } {\bf i'}} \right) & \left( \matrix{\text{x-comp} \\ \text{of } {\bf j'}} \right) & \left( \matrix{\text{x-comp} \\ \text{of } {\bf k'}} \right) \\ \left( \matrix{\text{y-comp} \\ \text{of } {\bf i'}} \right) & \left( \matrix{\text{y-comp} \\ \text{of } {\bf j'}} \right) & \left( \matrix{\text{y-comp} \\ \text{of } {\bf k'}} \right) \\ \left( \matrix{\text{z-comp} \\ \text{of } {\bf i'}} \right) & \left( \matrix{\text{z-comp} \\ \text{of } {\bf j'}} \right) & \left( \matrix{\text{z-comp} \\ \text{of } {\bf k'}} \right) } \right] \]
where "x-comp of \({\bf i'}\)" means the x-component of the \({\bf i'}\) unit vector. Pay close attention here to which terms have primes on them and which don't. Don't confuse this with "the x'-component" because "the x'-comp of \({\bf i'}\)" is simply 1. Yet another way to say this is, "the first component of the \({\bf i'}\) unit vector in the non-primed reference \(x, y, z\) coordinate system." Once again, this is just the transpose of the \({\bf Q}\) matrix.
Successive Rotations - Roe Convention
The 3-D rotation matrix can be viewed as a series of three successive rotations about coordinate axes. There must be dozens of variations of this since any combination of axes can be chosen in any order to rotate about. One popular choice is the so-called Roe convention.As shown in the figure, it consists of (i) a rotation through angle \(\psi\) about the z-axis, then (ii) a rotation of angle \(\theta\) about the new y-axis (which has already rotated itself due to the first rotation about z), and finally, (iii) a second rotation of \(\phi\) about the now-tilted z-axis.
The Roe convention is very popular despite one key challenge it contains. That is... if \(\theta = 0\), then \(\psi\) and \(\phi\) become indistinguishable and only the sum of the two is what matters.
\[ \begin{eqnarray} {\bf R} & = & \left[ \matrix { \cos \psi & \! -\sin \psi & 0 \\ \sin \psi & \;\;\; \cos \psi & 0 \\ 0 & 0 & 1 } \right] \left[ \matrix { \;\;\; \cos \theta & 0 & \sin \theta \\ \;\; 0 & 1 & 0 \\ -\sin \theta & 0 & \cos \theta } \right] \left[ \matrix { \cos \phi & \! -\sin \phi & 0 \\ \sin \phi & \;\;\; \cos \phi & 0 \\ 0 & 0 & 1 } \right] \\ \\ \\ & = & \left[ \matrix { \cos \psi \cos \theta \cos \phi - \sin \psi \sin \phi & -\cos \psi \cos \theta \sin \phi - \sin \psi \cos \phi & \cos \psi \sin \theta \\ \sin \psi \cos \theta \cos \phi + \cos \psi \sin \phi & -\sin \psi \cos \theta \sin \phi + \cos \psi \cos \phi & \sin \psi \sin \theta \\ -\sin \theta \cos \phi & \;\;\; \sin \theta \sin \phi & \;\; \cos \theta } \right] \end{eqnarray} \]
This time, the rotation matrices are indeed written in the same order: \(\psi, \theta, \phi\).
Roe Angles Example
In the figure above, \(\psi = 60^\circ, \theta = 30^\circ,\) and \(\phi = 45^\circ\). These Roe angles give a coordinate transformation matrix equal to\[ \begin{eqnarray} {\bf R} & = & \left[ \matrix { \cos 60^\circ \cos 30^\circ \cos 45^\circ - \sin 60^\circ \sin 45^\circ & -\cos 60^\circ \cos 30^\circ \sin 45^\circ - \sin 60^\circ \cos 45^\circ & \cos 60^\circ \sin 30^\circ \\ \;\;\; \sin 60^\circ \cos 30^\circ \cos 45^\circ + \cos 60^\circ \sin 45^\circ & -\sin 60^\circ \cos 30^\circ \sin 45^\circ + \cos 60^\circ \cos 45^\circ & \sin 60^\circ \sin 30^\circ \\ -\sin 30^\circ \cos 45^\circ & \;\;\; \sin 30^\circ \sin 45^\circ & \cos 30^\circ } \right] \\ \\ \\ & = & \left[ \matrix { -0.3062 & -0.9186 & 0.2500 \\ \;\;\; 0.8839 & -0.1768 & 0.4330 \\ -0.3536 & \;\;\; 0.3536 & 0.8660 } \right] \end{eqnarray} \]
Going In Reverse - Determining Roe Angles from a Rotation Matrix
Suppose you have a rotation matrix populated with values as shown here and would like to know what Roe transformation angles were responsible for producing the matrix.\[ {\bf R} = \left[ \matrix { R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} } \right] \]
The first and easiest step is to look at the \(R_{33}\) component. It is simply the cosine of \(\theta\), so \(\theta = \text{Cos}^{-1}(R_{33})\).
\[ {R_{23} \over R_{13}} = { \sin \psi \sin \theta \over \cos \psi \sin \theta } = { \sin \psi \over \cos \psi } = \tan \psi \] So
\[ \psi = \text{Tan}^{-1} \left( {R_{23} \over R_{13}} \right) \] The same process leads to
\[ \phi = \text{Tan}^{-1} \left({R_{32} \over -R_{31}} \right) \] So in summary
\[ \psi = \text{Tan}^{-1} \left( {R_{23} \over R_{13}} \right) \qquad \qquad \theta = \text{Cos}^{-1} \left( R_{33} \right) \qquad \qquad \phi = \text{Tan}^{-1} \left( {R_{32} \over -R_{31}} \right) \]
UNLESS!!!....... \(\theta\) proves to be very small! In this case, \(\sin \theta\) will be very small and therefore, so will \(R_{31}, R_{32}, R_{13}\), and \(R_{23}\) because all these terms contain \(\sin \theta\). This can lead to major round-off errors in any such calculations.
Fortunately, the solution for this (\(\theta \rightarrow 0\)) is to recall that \(\psi\) and \(\phi\) become indistinguishable from each other. This permits \(\phi\) to be set to zero, and \(\psi\) to be computed according to \(\psi = \text{Sin}^{-1}(R_{21})\).
Example: Roe Angles from Matrix
Let's start with the matrix in the previous example and work backwards.\[ {\bf R} = \left[ \matrix { -0.3062 & -0.9186 & 0.2500 \\ \;\;\; 0.8839 & -0.1768 & 0.4330 \\ -0.3536 & \;\;\; 0.3536 & 0.8660 } \right] \]
Start with the \(R_{33}\) term to determine \(\theta\).
\[ \theta = \text{Cos}^{-1}(R_{33}) = \text{Cos}^{-1}(0.8660) = 30^\circ \]
Since \(\theta\) is not near zero, \(\psi\) and \(\phi\) can be computed as follows.
\[ \psi = \text{Tan}^{-1}\left({R_{23} \over R_{13}}\right) = \text{Tan}^{-1}\left({0.4330 \over 0.2500}\right) = 60^\circ \]
\[ \phi = \text{Tan}^{-1}\left({R_{32} \over -R_{31}}\right) = \text{Tan}^{-1}\left({0.3536 \over 0.3536}\right) = 45^\circ \]
So as expected, the original values are recovered: \( \psi = 60^\circ, \; \theta = 30^\circ,\) and \(\phi = 45^\circ\).
Rotation About An Axis
Yet another way of specifying the rotation matrix is through a rotation axis vector, \({\bf p}\), and a rotation angle, \(\alpha\), about the \({\bf p}\) axis.In this case, the rotation matrix is written as
\[ {\bf R} = \cos \alpha \; {\bf I} + (1 - \cos \alpha) {\bf p} \otimes {\bf p} - \sin \alpha \; {\bf P} \]
with
\[ {\bf P} = \left[ \matrix { \;\;\; 0 & \;\;\; p_3 & -p_2 \\ -p_3 & \;\; 0 & \;\;\; p_1 \\ \;\;\; p_2 & -p_1 & \;\;\; 0 } \right] \]
Writing the matrix out gives
\[ {\bf R} = \left[ \matrix { \cos \alpha + (1-\cos \alpha) p^2_1 & (1 - \cos \alpha) p_1 p_2 - \sin \alpha \; p_3 & (1 - \cos \alpha) p_1 p_3 + \sin \alpha \; p_2 \\ (1 - \cos \alpha) p_2 p_1 + \sin \alpha \; p_3 & \cos \alpha + (1-\cos \alpha) p^2_2 & (1 - \cos \alpha) p_2 p_3 - \sin \alpha \; p_1 \\ (1 - \cos \alpha) p_3 p_1 - \sin \alpha \; p_2 & (1 - \cos \alpha) p_3 p_2 + \sin \alpha \; p_1 & \cos \alpha + (1-\cos \alpha) p^2_3 } \right] \]
As usual, this can be written quite concisely in tensor notation
\[ R_{ij} = \cos \alpha \; \delta_{ij} + (1 - \cos \alpha) p_i p_j - \sin \alpha \; \epsilon_{ijk} \; p_k \]
Note the similarity to the tensor equation of \({\bf Q}\). The only difference is the + or - in front of \(\sin \alpha\).
\[ Q_{ij} = \cos \alpha \; \delta_{ij} + (1 - \cos \alpha) p_i p_j + \sin \alpha \; \epsilon_{ijk} \; p_k \]
It is very important to recognize that \({\bf p}\) is a unit vector. Using any other length will lead to incorrect results.
Also, it's actually more common to use \(\theta\) or \(\phi\) as the rotation angle instead of \(\alpha\). But \(\alpha\) is being used here to minimize confusion with \(\psi, \theta,\) and \(\phi\) used as the Roe convention angles.
It is easy to visualize the coordinate rotations in this method. For example, the 2-D case can be reproduced by noting that the rotation is about the z-axis, so the vector is \({\bf p} = (0, 0, 1)\). This leads to
\[ {\bf R} = \left[ \matrix { \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \;\;\; \cos \alpha & 0 \\ 0 & 0 & 1 } \right] \]
\[ \alpha = \text{Cos}^{-1} \left\{ {1 \over 2} \Big[ \text{tr}({\bf R}) - 1 \Big] \right\} \]
Once \(\alpha\) is determined, the components of \({\bf p}\) are computed by
\[ p_1 = { R_{32} - R_{23} \over 2 \sin \alpha } \qquad \qquad p_2 = { R_{13} - R_{31} \over 2 \sin \alpha } \qquad \qquad p_3 = { R_{21} - R_{12} \over 2 \sin \alpha } \]
The three equations can be conveniently summarized in tensor notation as
\[ p_i = { - \epsilon_{ijk} R_{jk} \over 2 \sin \alpha } \]
Note that \({\bf p}\) becomes undefined when \(\alpha = 0\). This means, "the axis you rotate about doesn't matter if you don't rotate in the first place."
Backing Out P and α
Determine the single rotation, \({\bf p}\) and \(\alpha\), that is equivalent to that produced by the Roe angles used earlier: \(\psi = 60^\circ, \theta = 30^\circ,\) and \(\phi = 45^\circ\).Recall that the Roe angles \(\psi = 60^\circ, \theta = 30^\circ,\) and \(\phi = 45^\circ\) lead to
\[ {\bf R} = \left[ \matrix { -0.3062 & -0.9186 & 0.2500 \\ \;\;\; 0.8839 & -0.1768 & 0.4330 \\ -0.3536 & \;\;\; 0.3536 & 0.8660 } \right] \]
Solving for \(\alpha\) gives
\[ \alpha = \text{Cos}^{-1} \left\{ {1 \over 2} \Big[ -0.3062 - 0.1768 +0.8660 - 1 \Big] \right\} = 108^\circ \]
Solving for \({\bf p}\) gives
\[ p_1 = { 0.3536 - 0.4330 \over 2 \; \sin 108^\circ} = -0.0417 \]
\[ p_2 = { 0.2500 - (-0.3536) \over 2 \; \sin 108^\circ} = 0.3173 \]
\[ p_3 = { 0.8839 - (-0.9186) \over 2 \; \sin 108^\circ} = 0.9475 \]
So the Roe angles \(\psi = 60^\circ, \theta = 30^\circ,\) and \(\phi = 45^\circ\) are equivalent to a single rotation of \(108^\circ\) about the axis given by \({\bf p} = (-0.0417\), \(0.3173\), \(0.9475)\). Both sets lead to the same rotation of an object.
Inverses and Transposes
All rotation matrices possess a rather remarkable property - their transpose is their inverse. So it becomes trivial to compute the inverse of such a matrix.\[ {\bf R}^T = {\bf R}^{-1} \qquad \text{so} \qquad {\bf R}^T \cdot {\bf R} = {\bf I} \]
Dot Product Example
The above \({\bf R}\) matrix is\[ {\bf R} = \left[ \matrix { -0.3062 & -0.9186 & 0.2500 \\ \;\;\; 0.8839 & -0.1768 & 0.4330 \\ -0.3536 & \;\;\; 0.3536 & 0.8660 } \right] \]
Multiply it by its transpose to demonstrate that the result is the identity matrix and therefore, its transpose must also be its inverse.
\[ {\bf R}^T \cdot {\bf R} = \left[ \matrix { -0.3062 & \;\;\; 0.8839 & -0.3536 \\ -0.9186 & -0.1768 & \;\;\; 0.3536 \\ \;\;\; 0.2500 & \;\;\; 0.4330 & \;\;\; 0.8660 } \right] \; \left[ \matrix { -0.3062 & -0.9186 & 0.2500 \\ \;\;\; 0.8839 & -0.1768 & 0.4330 \\ -0.3536 & \;\;\; 0.3536 & 0.8660 } \right] = \left[ \matrix { 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 } \right] \]