Search Continuum Mechanics Website

Hooke's Law

 home > introductory mechanics > hooke's law

Introduction

We have talked about Hooke's Law some already, and used it for tensor notation exercises and examples. Hooke's Law describes linear material behavior. It is commonly used for isotropic materials (same behavior in all directions), but can also be extended to anisotropic materials. It is in fact the 1st order linearization of any hyperelastic material Law, including nonlinear ones. So it can be applied to rubber as long as the strains are small. And it is the standard for metals in the elastic range.

---

Normal Components

The first step in getting to the full model is to start with simple uniaxial tension/compression. In this case, the relationship is

\[ \sigma = E \, \epsilon \]
That's simple enough. It is linear because the stress and strain terms are all first-order. Keep in mind that \(E\) has units of stress just like \(\sigma\) because strain is unitless.

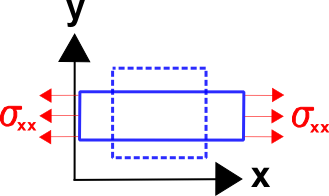
The next step is to generalize this for the case of multiple dimensions. For starters, decide that the tension/compression direction is \(x\). So the stress and strain in the above equation will be in the \(x\) direction. Also write the above equation a little differently as

\[ \epsilon_{xx} = {1 \over E} \sigma_{xx} \]
So far, so good. Now add some complexity. Add an additional normal stress in the \(y\) direction. Any tensile stress in the \(y\) direction will cause the strain in the \(x\) direction to decrease. So modify the above equation as follows.

\[ \epsilon_{xx} = {1 \over E} \sigma_{xx} - B \, \sigma_{yy} \]
In this case, \(B\) is a material property just like \(E\) and requires a lab test to determine. Nevertheless, using \(B\) in this form is not very practical. It is much more useful to express \(B\) as a fraction of \((1 / E)\). Something like

\[ \epsilon_{xx} = {1 \over E} \sigma_{xx} - f {1 \over E} \sigma_{yy} \]
where \(f\) is the "fraction". It is a number between 0 and 1 because material behavior dictates it to be so. It is less than 1 because strains in the \(x\) direction, \(\epsilon_{xx}\), are less sensitive to stresses in the \(y\) direction, \(\sigma_{yy}\), than they are to stresses in the \(x\) direction, \(\sigma_{xx}\).

Except that instead of using \(f\) as the symbol, use \(\nu\) instead. This is Poisson's ratio. It is the ratio of the sensitivity of strain to two stresses, one in line with the strain, and the other perpendicular to it.

We will see that Poisson's ratio is 1/2 for incompressible materials such as rubber. It is pretty consistently 1/3 for face-centered-cubic (FCC) materials like aluminum, nickel, and copper. And it is about 0.3 for steel.

So the above equation becomes

\[ \epsilon_{xx} = {1 \over E} \big[ \sigma_{xx} - \nu \, \sigma_{yy} \big] \]
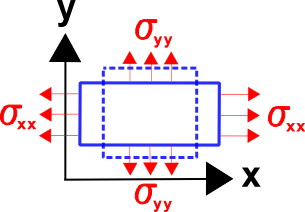
And now add in a \(\sigma_{zz}\) to the mix. If the material is isotropic, then the response of \(\epsilon_{xx}\) to \(\sigma_{zz}\) will be exactly the same as \(\sigma_{yy}\). So the equation can be written as

\[ \epsilon_{xx} = {1 \over E} \big[ \sigma_{xx} - \nu \left( \sigma_{yy} + \sigma_{zz} \big) \right] \]
This is the complete Hooke's Law, at least for \(\epsilon_{xx}\). It is also the defining equation for Poisson's ratio (not \(-\epsilon_{yy} / \epsilon_{xx}\) by the way).

POISSON RATIOS
Material	Poisson's Ratio	Comments
Foams	~0	Negligible effect
Steels	~0.3	Varies by a few % among steels
Aluminum	0.33	Face centered cubic (FCC) metals
Copper	0.33
Nickel	0.33
Rubber	0.50	Incompressible

The complete set of equations are

\[ \epsilon_{xx} = {1 \over E} \big[ \sigma_{xx} - \nu \, ( \sigma_{yy} + \sigma_{zz} ) \big] \] \[ \epsilon_{yy} = {1 \over E} \big[ \sigma_{yy} - \nu \, ( \sigma_{xx} + \sigma_{zz} ) \big] \] \[ \epsilon_{zz} = {1 \over E} \big[ \sigma_{zz} - \nu \, ( \sigma_{xx} + \sigma_{yy} ) \big] \]

---

Shear Components

We've worked out Hooke's Law for the normal components. We will now use them to develop the relationship between the shear stresses and strains. Start with a shear stress, \(\tau_{xy}\), and shear strain, \(\gamma_{xy}\), and rotate them 45° to get the principal values.

For the shear stress

\[ \left[ \matrix { 0 & \tau_{xy} \\ \tau_{xy} & 0 } \right] \qquad \matrix { 45^\circ \\ \text{transform} \\ \longrightarrow \; } \qquad \left[ \matrix { \tau_{xy} & 0 \\ 0 & -\tau_{xy} } \right] \]
and the shear strain

\[ \left[ \matrix { 0 & \gamma_{xy} / 2 \\ \gamma_{xy} / 2 & 0 } \right] \qquad \matrix { 45^\circ \\ \text{transform} \\ \longrightarrow \; } \qquad \left[ \matrix { \gamma_{xy} / 2 & 0 \\ 0 & -\gamma_{xy} / 2 } \right] \]
So the principal values are

\[ \sigma_1 = \tau_{xy} \qquad \qquad \sigma_2 = -\tau_{xy} \qquad \qquad \epsilon_1 = \gamma_{xy} / 2 \qquad \qquad \epsilon_2 = -\gamma_{xy} / 2 \]
Plugging the positive principal strain into Hooke's Law gives

\[ \epsilon_1 = {1 \over E} \big[ \sigma_1 - \nu \left( \sigma_2 + \sigma_3 \right) \big] \]

\[ {\gamma_{xy} \over 2} = {1 \over E} \big[ \tau_{xy} - \nu \left( -\tau_{xy} + 0 \right) \big] \]
Rearrange to get

\[ \tau_{xy} = {E \over 2 (1 + \nu) } \gamma_{xy} \]
And this leads to the expression for the shear modulus.

\[ G = {\tau_{xy} \over \gamma_{xy}} = {E \over 2 (1 + \nu) } \]

---

Bulk Modulus

Return to the three equations for normal strain in terms of normal stress.

\[ \epsilon_{xx} = {1 \over E} \big[ \sigma_{xx} - \nu \, ( \sigma_{yy} + \sigma_{zz} ) \big] \] \[ \epsilon_{yy} = {1 \over E} \big[ \sigma_{yy} - \nu \, ( \sigma_{xx} + \sigma_{zz} ) \big] \] \[ \epsilon_{zz} = {1 \over E} \big[ \sigma_{zz} - \nu \, ( \sigma_{xx} + \sigma_{yy} ) \big] \]
Add the three equations together.

\[ \epsilon_{xx} + \epsilon_{yy} + \epsilon_{zz} = { (1 - 2 \nu) \over E} ( \sigma_{xx} + \sigma_{yy} + \sigma_{zz} ) \]
But \((\epsilon_{xx} + \epsilon_{yy} + \epsilon_{zz})\) is the volumetric strain, \(\epsilon_\text{Vol} = \Delta V / V\). We will discuss this at length in the next chapter on strain and deformations.

And \((\sigma_{xx} + \sigma_{yy} + \sigma_{zz})\) is three times the hydrostatic stress, \(3 \, \sigma_\text{Hyd}\). Note that hydrostatic stress is simply the average of the diagonal components and is the pressure your ears feel when you go deep under water.

So the equation becomes

\[ \epsilon_\text{Vol} = { 3 (1 - 2 \nu) \over E} \sigma_\text{Hyd} \]
And the ratio of the \(\sigma_\text{Hyd}\) to \(\epsilon_\text{Vol}\) is the bulk modulus, \(K\).

\[ K = { \sigma_\text{Hyd} \over \epsilon_\text{Vol} } = { E \over 3 (1 - 2 \nu) } \]
And a little more rearrangement gives

\[ {E \over K} = 3 (1 - 2 \nu) \]
This is the important relationship between tensile modulus and bulk modulus. Although the bulk modulus for rubber is not large, it is nevertheless much larger than the tensile modulus. So the ratio of the two is very small. This dictates that the Poisson Ratio for rubber must be 0.5. This is so that the RHS term, \(3 ( 1 - 2 \nu )\), equals zero.

---

Matrix & Tensor Notation

Hooke's Law can be written in matrix notation as

\[ \boldsymbol{\epsilon} = {1 \over E} \left[ (1 + \nu) \boldsymbol{\sigma} - \nu \; {\bf I} \; \text{tr}(\boldsymbol{\sigma}) \right] \]
and in tensor notation as

\[ \epsilon_{ij} = {1 \over E} \left[ (1 + \nu) \sigma_{ij} - \nu \; \delta_{ij} \; \sigma_{kk} \right] \]
Writing all the matrices out gives

\[ \left[ \matrix { \epsilon_{11} & \epsilon_{12} & \epsilon_{13} \\ \epsilon_{21} & \epsilon_{22} & \epsilon_{23} \\ \epsilon_{31} & \epsilon_{32} & \epsilon_{33} } \right] = {1 \over E} \left\{ (1 + \nu) \left[ \matrix { \sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_{22} & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_{33} } \right] - \nu \, ( \sigma_{11} + \sigma_{22} + \sigma_{33} ) \left[ \matrix { 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1} \right] \right\} \]
The individual component equations all together are

\[ \epsilon_{11} = {1 \over E} \left[ (1 + \nu) \sigma_{11} - \nu \; (\sigma_{11} + \sigma_{22} + \sigma_{33}) \right] \qquad \qquad \epsilon_{12} = {1 \over E} \left[ (1 + \nu) \sigma_{12} \right] \] \[ \epsilon_{22} = {1 \over E} \left[ (1 + \nu) \sigma_{22} - \nu \; (\sigma_{11} + \sigma_{22} + \sigma_{33}) \right] \qquad \qquad \epsilon_{13} = {1 \over E} \left[ (1 + \nu) \sigma_{13} \right] \] \[ \epsilon_{33} = {1 \over E} \left[ (1 + \nu) \sigma_{33} - \nu \; (\sigma_{11} + \sigma_{22} + \sigma_{33}) \right] \qquad \qquad \epsilon_{23} = {1 \over E} \left[ (1 + \nu) \sigma_{23} \right] \]
but then clean up into the familiar forms

\[ \epsilon_{11} = {1 \over E} \left[ \sigma_{11} - \nu \; (\sigma_{22} + \sigma_{33}) \right] \qquad \qquad \epsilon_{12} = {(1 + \nu) \over E} \sigma_{12} \] \[ \epsilon_{22} = {1 \over E} \left[ \sigma_{22} - \nu \; (\sigma_{11} + \sigma_{33}) \right] \qquad \qquad \epsilon_{13} = {(1 + \nu) \over E} \sigma_{13} \] \[ \epsilon_{33} = {1 \over E} \left[ \sigma_{33} - \nu \; (\sigma_{11} + \sigma_{22}) \right] \qquad \qquad \epsilon_{23} = {(1 + \nu) \over E} \sigma_{23} \]

---

Inverting Hooke's Law

This will demonstrate how to invert Hooke's Law from strain-as-a-function-of-stress to stress-as-a-function-of-strain.

Returning to the fundamental equation...

\[ \epsilon_{ij} = {1 \over E} \left[ (1 + \nu) \sigma_{ij} - \nu \; \delta_{ij} \; \sigma_{kk} \right] \]
It is easy to solve for \(\sigma_{ij}\) to get

\[ \sigma_{ij} = {1 \over (1 + \nu)} \left[ E \; \epsilon_{ij} + \nu \; \delta_{ij} \; \sigma_{kk} \right] \]
Multiply both sides by \(\delta_{ij}\)

\[ \delta_{ij} \sigma_{ij} = {1 \over (1 + \nu)} \left[ E \; \delta_{ij} \; \epsilon_{ij} + \nu \; \delta_{ij} \; \delta_{ij} \; \sigma_{kk} \right] \]
and simplify

\[ \sigma_{kk} = {E \; \epsilon_{jj} \over (1 - 2 \nu)} \]
which is the simple clean equation we need to insert back into

\[ \sigma_{ij} = {1 \over (1 + \nu)} \left[ E \; \epsilon_{ij} + \nu \; \delta_{ij} \; \sigma_{kk} \right] \]
to obtain

\[ \sigma_{ij} = {E \over (1 + \nu)} \left[ \epsilon_{ij} + { \nu \over (1 - 2 \nu)} \delta_{ij} \epsilon_{kk} \right] \]
Note that in this equation, it is impossible to calculate the stress tensor given a strain tensor if the material is incompressible because \(\nu = 0.5\).

---

Stiffness Tensor

The stiffness tensor is a 4th rank quantity (3x3x3x3) that relates stress to strain.

\[ \boldsymbol{\sigma} = {\bf C} : \boldsymbol{\epsilon} \qquad \qquad \sigma_{ij} = C_{ijkl} \epsilon_{kl} \]
We will see on the thermodynamics page that the stiffness tensor is fundamentally the second partial derivative of the Helmholtz free energy with respect to the elastic portion of the Green strain tensor.

\[ {\bf C} = \rho_o \, {\partial^2 \Psi \over \partial \boldsymbol{\epsilon}^\text{el} \partial \boldsymbol{\epsilon}^\text{el} } \]
But alas, this is not very useful when doing most analyses. Instead, it is much easier to take the derivative of Hooke's Law. Start by writing Hooke's Law in tensor notation.

\[ \sigma_{ij} = {E \over (1 + \nu)} \left[ \epsilon_{ij} + { \nu \over (1 - 2 \nu)} \delta_{ij} \, \epsilon_{mm} \right] \]
And take the derivative as follows.

\[ \begin{eqnarray} C_{ijkl} & = & {\partial \sigma_{ij} \over \partial \epsilon_{kl} } \\ \\ \\ & = & {\partial \over \partial \epsilon_{kl} } \left\{ {E \over (1 + \nu)} \left[ \epsilon_{ij} + { \nu \over (1 - 2 \nu)} \delta_{ij} \, \epsilon_{mm} \right] \right\} \\ \\ \\ & = & {E \over (1 + \nu)} \left[ \delta_{ik} \, \delta_{jl} + { \nu \over (1 - 2 \nu)} \delta_{ij} \, \delta_{mk} \, \delta_{ml} \right] \end{eqnarray} \]
The Kronecker deltas appear because

\[ {\partial \epsilon_{ij} \over \partial \epsilon_{kl} } = \delta_{ik} \, \delta_{jl} \qquad \qquad \text{and} \qquad \qquad {\partial \epsilon_{mm} \over \partial \epsilon_{kl} } = \delta_{mk} \, \delta_{ml} \]
Except... all this is wrong!!! WRONG, WRONG, WRONG!!!

The problem is that the equation for the stiffness tensor is not symmetric with respect to \(i\) and \(j\), as \(\sigma_{ij}\) is, and with respect to \(k\) and \(l\), as \(\epsilon_{kl}\) is.

You can see this by looking at the first term above, \(\delta_{ik} \, \delta_{jl}\). This term is not symmetric with respect to \(i\) and \(j\) because swapping them gives \(\delta_{jk} \, \delta_{il}\), which is a different, and therefore not symmetric result.

The problem is way back with the original Hooke's Law equation.

\[ \sigma_{ij} = {E \over (1 + \nu)} \left[ \epsilon_{ij} + { \nu \over (1 - 2 \nu)} \delta_{ij} \, \epsilon_{mm} \right] \]
The issue here is that this equation does not force the tensors to be symmetric. The stress and strain tensors could easily be nonsymmetric and still satisfy Hooke's Law. So before taking the derivative with respect to strain, the equation can be modified to force symmetry. This is accomplished by replacing \(\epsilon_{ij}\) with

\[ \epsilon_{ij} \; \rightarrow \; { \epsilon_{ij} + \epsilon_{ji} \over 2 } \]
So Hooke's Law becomes

\[ \sigma_{ij} = {E \over (1 + \nu)} \left[ { 1 \over 2} (\epsilon_{ij} + \epsilon_{ji}) + { \nu \over (1 - 2 \nu)} \delta_{ij} \, \epsilon_{mm} \right] \]
This equation forces the stress tensor to be symmetric. Now taking the derivative of this gives

\[ \begin{eqnarray} C_{ijkl} & = & {\partial \sigma_{ij} \over \partial \epsilon_{kl} } \\ \\ \\ & = & {\partial \over \partial \epsilon_{kl} } \left\{ {E \over (1 + \nu)} \left[ { 1 \over 2} (\epsilon_{ij} + \epsilon_{ji}) + { \nu \over (1 - 2 \nu)} \delta_{ij} \, \epsilon_{mm} \right] \right\} \\ \\ \\ & = & {E \over (1 + \nu)} \left[ {1 \over 2} ( \delta_{ik} \, \delta_{jl} + \delta_{jk} \, \delta_{il} ) + { \nu \over (1 - 2 \nu)} \delta_{ij} \, \delta_{mk} \, \delta_{ml} \right] \\ \\ \\ & = & {E \over (1 + \nu)} \left[ {1 \over 2} ( \delta_{ik} \, \delta_{jl} + \delta_{jk} \, \delta_{il} ) + { \nu \over (1 - 2 \nu)} \delta_{ij} \, \delta_{kl} \right] \end{eqnarray} \]
This is now symmetric with respect to \(i\) and \(j\) and with respect to \(k\) and \(l\).

---

Deviatoric Stress & Strain

This section develops a fascinating relationship between deviatoric stress and strain based on Hooke's Law. Start with the usual relationship.

\[ \epsilon_{ij} = {1 \over E} \left[ (1 + \nu) \sigma_{ij} - \nu \, \delta_{ij} \sigma_{kk} \right] \]
Multiplying both sides by \(\delta_{ij}\) gives

\[ \epsilon_{kk} = { (1 - 2 \nu) \over E} \sigma_{kk} \]
And then multiply both sides by \({ 1 \over 3} \delta_{ij}\) again to get

\[ { 1 \over 3} \delta_{ij} \epsilon_{kk} = {(1 - 2 \nu) \over 3 E} \delta_{ij} \sigma_{kk} \]
This results in an equation relating the hydrostatic stress and strain values.

Now subtract it from the original Hooke's Law equation to get

\[ \begin{eqnarray} \epsilon_{ij} - { 1 \over 3} \delta_{ij} \epsilon_{kk} & \, = \, & { (1 + \nu) \over E} \sigma_{ij} - { \nu \over E} \, \delta_{ij} \sigma_{kk} - {(1 - 2 \nu) \over 3 E} \delta_{ij} \sigma_{kk} \\ \\ \\ & \, = \, & { (1 + \nu) \over E} \sigma_{ij} - { 1 \over E} \left( \nu + {1 - 2 \nu \over 3} \right) \delta_{ij} \sigma_{kk} \\ \\ \\ & \, = \, & { (1 + \nu) \over E} \sigma_{ij} - { 1 \over 3} {(1 + \nu) \over E} \delta_{ij} \sigma_{kk} \\ \\ \\ & \, = \, & { (1 + \nu) \over E} \big( \sigma_{ij} - { 1 \over 3} \delta_{ij} \sigma_{kk} \big) \\ \end{eqnarray} \]
The remarkable result is that both sides of the equation contain a deviatoric tensor result. The equation can be summarized as

\[ \epsilon'\!_{ij} = { ( 1 + \nu ) \over E} \sigma'\!_{ij} \]
But \({ (1 + \nu) \over E }\) is \({1 \over 2G}\), so the equation can be further simplified to

\[ \epsilon'\!_{ij} = { 1 \over 2 G} \sigma'\!_{ij} \]
So the deviatoric stress and strain are directly proportional to each other. The amazing thing here is that this is always true for Hooke's Law, always, even for the normal strain components.

For what it's worth, the equation can also be written as

\[ \sigma'\!_{ij} = 2 \, G \, \epsilon'\!_{ij} \]