Introduction
Velocity gradients are absolutely essential to analyses involving path dependent materials, such as the plastic deformation of metals. Granted, rubber can usually be treated as hyperelastic, which implies no path dependence. Although viscous damping of rubber can be addressed with velocity gradients. Regardless, velocity gradients are useful to better understanding deformations and especially useful to determining energetically conjugate stresses and strains, which is important to all materials.Velocity Gradient
The velocity gradient is to velocities what the deformation gradient is to displacements. The velocity gradient is represented by \({\bf L}\) and defined by\[ {\bf L} = {\partial {\bf v} \over \partial {\bf x} } = \left[ \matrix{ {\partial v_x \over \partial x} & {\partial v_x \over \partial y} & {\partial v_x \over \partial z} \\ \\ {\partial v_y \over \partial x} & {\partial v_y \over \partial y} & {\partial v_y \over \partial z} \\ \\ {\partial v_z \over \partial x} & {\partial v_z \over \partial y} & {\partial v_z \over \partial z} } \right] \]
Note that the derivative is with respect to the current coordinates, \({\bf x}\), not the reference coordinates, \({\bf X}\). This means it is an Eulerian quantity rather than a Lagrangian quantity. The velocity gradient can also be written as
\[ L_{ij} = {\partial v_i \over \partial x_j } \] or as
\[ L_{ij} = v_{i,j} \]
Although this notation relies on the reader knowing that the "\(j\)" represents \(x_j\) instead of \(X_j\).
Velocity Gradient Example
The velocity gradient is ideally suited to applications involving fluids. With fluids, it is impossible to specify \({\bf X}\). This leaves \({\bf x}\) as the only practical coordinates to describe the velocity field in.Suppose the velocity field is
\[ {\bf v} = ({1 \over 5-x}, {-y \; \over 10}, 0) \]
This gives the velocity of any particle in the fluid as a function of the particle's position at that instant.
The velocity gradient is
\[ {\bf L} = \left[ \matrix{ {1 \; \over (5-x)^2} & 0 & & 0 \\ 0 & {-1 \; \over 10} & & 0 \\ \\ 0 & 0 & & 0 } \right] \]
\[ \dot {\bf F} \; = \; {d \over dt} \left( {\partial {\bf x} \over \partial {\bf X}} \right) \; = \; {\partial \over \partial {\bf X}} \left( {d{\bf x} \over dt} \right) \; = \; {\partial {\bf v} \over \partial {\bf X}} \]
\[ \dot {\bf F} \; = \; {\partial {\bf v} \over \partial {\bf X}} \; = \; \left( {\partial {\bf v} \over \partial {\bf x}} \right) \left( {\partial {\bf x} \over \partial {\bf X}} \right) \]
The first partial derivative is \({\bf L}\) and the second is simply \({\bf F}\). So the above equation can be written as
\[ \dot {\bf F} = {\bf L} \cdot {\bf F} \]
Post multiplying both sides by \({\bf F}^{-1}\) gives the equation for \({\bf L}\) in terms of \({\bf F}\).
\[ {\bf L} = \dot {\bf F} \cdot {\bf F}^{-1} \]
The two equations above are incredibly useful, although that is probably not apparent at this point. With the one immediately above, it is possible to calculate the Eulerian quantity \({\bf L}\) by using only the Lagrangian quantity, \({\bf F}\).
Tension Velocity Gradient Example
Recall the Almansi strain example in which the displacements were expressed in terms of \({\bf X}\) and then \({\bf x}\). This time, in order to calculate velocity gradients, we must first have velocities.So this time, let
\[ x = \left( {X \over L_o} \right) L_F \]
If the object is being stretched such that
\[ L_F = L_o + A\,t \]
where \(A\) is any positive constant, then
\[ x = \left( {X \over L_o} \right) (L_o + A\,t) \]
and \(v_x\) is \({dx \over dt}\), so this gives
\[ v_x = \left( {X \over L_o} \right) A \]
This is nice, but no help to a velocity gradient because the velocity is not expressed as a function of \(x\). But this can be overcome by combining the two above equations to get
\[ v_x = {A x \over L_o + A\,t} \]
And now the velocity gradient can be evaluated.
\[ L_{11} = {\partial v_x \over \partial x} = {A \over L_o + A\,t} = {A \over L_F} \]
and
\[ {\bf L} = \left[ \matrix{ A/L_F & 0 \;\; & 0 \\ 0 & 0 \;\; & 0 \\ 0 & 0 \;\; & 0 } \right] \]
This result emphasizes how a velocity gradient is an Eulerian quantity because \(L_{11} = {A \over L_F}\) rather than \({A \over L_o}\). As the object stretches, \(L_F\) increases with time and \(L_{11}\) decreases.
Velocity Gradient Using F
This time, repeat the above example, but use \({\bf L} = \dot {\bf F} \cdot {\bf F}^{-1}\) to demonstrate that it gives the same result.Recall that
\[ x = \left( {X \over L_o} \right) (L_o + A\,t) = \left( {X \over L_o} \right) L_F \]
The deformation gradient is
\[ {\bf F} = \left[ \matrix{ {L_o + A\,t \over L_o} & 0 & \;\;0 \\ \\ 0 & 1 & \;\;0 \\ \\ 0 & 0 & \;\;1 } \right] \]
and its inverse is
\[ {\bf F}^{-1} = \left[ \matrix{ {L_o \over L_o+A\,t} & 0 & \;\;0 \\ \\ 0 & 1 & \;\;0 \\ \\ 0 & 0 & \;\;1 } \right] = \left[ \matrix{ {L_o \over L_F} & 0 & \;\;0 \\ \\ 0 & 1 & \;\;0 \\ \\ 0 & 0 & \;\;1 } \right] \]
We also need \(\dot {\bf F}\). It is
\[ \dot {\bf F} = \left[ \matrix{ {A \over L_o} & 0 & \;\;0 \\ \\ 0 & 0 & \;\;0 \\ \\ 0 & 0 & \;\;0 } \right] \]
So the product of \(\dot {\bf F}\) and \({\bf F}^{-1}\) gives
\[ {\bf L} = \dot {\bf F} \cdot {\bf F}^{-1} = \left[ \matrix{ {A \over L_o} & 0 & \;\;0 \\ \\ 0 & 0 & \;\;0 \\ \\ 0 & 0 & \;\;0 } \right] \left[ \matrix{ {L_o \over L_F} & 0 & \;\;0 \\ \\ 0 & 1 & \;\;0 \\ \\ 0 & 0 & \;\;1 } \right] = \left[ \matrix{ {A \over L_F} & 0 & \;\;0 \\ \\ 0 & 0 & \;\;0 \\ \\ 0 & 0 & \;\;0 } \right] \]
Which is identical to the previous example.
Velocity Gradients and Abaqus UMATS
The Abaqus finite element package has a feature called a "UMAT," which is short for USER MATERIAL subroutine. This subroutine gives the user an opportunity to write a subroutine that calculates the stress state in a material given the deformation gradients at the beginning, \({\bf F}_t\), and end \({\bf F}_{t+\Delta t}\), of a time step. (Abaqus documentation here.)One could treat the rubber as hyperelastic and calculate the stress based solely on \({\bf F}_{t+\Delta t}\). Or one could use both deformation gradients to compute the velocity gradient and use this to include viscoelastic or hysteretic damping in the stress calculation.
For example, suppose that Abaqus executes a time step during a transient simulation that is \(\Delta t = 0.1 \text{sec}\). At the beginning of the time step (which was just the end of the previous step), the deformation gradient is
\[ {\bf F}_t = \left[ \matrix{ 1.30 & 0 & 0 \\ 0 & 0.90 & 0 \\ 0 & 0 & 0.90 } \right] \]
And at the end of the step, it is
\[ {\bf F}_{t+\Delta t} = \left[ \matrix{ 1.40 & 0 & 0 \\ 0 & 0.85 & 0 \\ 0 & 0 & 0.85 } \right] \]
So \(\dot {\bf F}\) is
\[ \begin{eqnarray} \dot {\bf F} & = & {1 \over \Delta t} \left( {\bf F}_{t+\Delta t} - {\bf F}_t \right) \\ \\ \\ & = & {1 \over 0.1} \left( \left[ \matrix{ 1.40 & 0 & 0 \\ 0 & 0.85 & 0 \\ 0 & 0 & 0.85 } \right] - \left[ \matrix{ 1.30 & 0 & 0 \\ 0 & 0.90 & 0 \\ 0 & 0 & 0.90 } \right] \right) \\ \\ \\ & = & \left[ \matrix{ 1.0 & 0 & 0 \\ 0 & -0.5 & 0 \\ 0 & 0 & -0.5 } \right] \end{eqnarray} \]
We need the inverse of a deformation gradient as well. Take the inverse of the later one.
\[ {\bf F}^{-1} = \left[ \matrix{ 1.40 & 0 & 0 \\ 0 & 0.85 & 0 \\ 0 & 0 & 0.85 } \right]^{-1} = \left[ \matrix{ 0.7143 & 0 & 0 \\ 0 & 1.1765 & 0 \\ 0 & 0 & 1.1765 } \right] \]
So \({\bf L}\) is
\[ {\bf L} = \dot {\bf F} \cdot {\bf F}^{-1} = \left[ \matrix{ 1.0 & 0 & 0 \\ 0 & -0.5 & 0 \\ 0 & 0 & -0.5 } \right] \left[ \matrix{ 0.714 & 0 & 0 \\ 0 & 1.177 & 0 \\ 0 & 0 & 1.177 } \right] = \left[ \matrix{ 0.714 & \;\;\;0 & \;\;\;0 \\ 0 & -0.588 & \;\;\;0 \\ 0 & \;\;\;0 & -0.588 } \right] \]
Rate of Deformation and Spin Tensors
\[ {\bf L} = {1 \over 2} \left( {\bf L} + {\bf L}^T \right) + {1 \over 2} \left( {\bf L} - {\bf L}^T \right) \]
The first term, \(( {\bf L} + {\bf L}^T ) / 2\), is symmetric and looks and behaves very much like the small strain tensor discussed earlier, except of course that it involves velocities rather than displacements. It is in fact a strain rate tensor in an Eulerian context. But it is formally called the Rate of Deformation Tensor, and assigned the symbol, \({\bf D}\). (I have never, ever seen it called a "deformation rate tensor".) So \({\bf D}\) is defined as
\[ {\bf D} = {1 \over 2} \left( {\bf L} + {\bf L}^T \right) \]
The second term, \( ( {\bf L} - {\bf L}^T ) / 2\), is a new animal. It is an antisymmetric tensor that looks and behaves somewhat different than anything we've discussed to date. The antisymmetric part is called the spin tensor and given the letter, \({\bf W}\). We will see that it is directly related to the rate of rotation of an object, but not its deformation at all. It is defined as
\[ {\bf W} = {1 \over 2} \left( {\bf L} - {\bf L}^T \right) \]
So the velocity gradient equation can be written as
\[ {\bf L} = {\bf D} + {\bf W} \]
The components of the rate of deformation tensor, \({\bf D}\), are
\[ {\bf D} = \left[ \matrix{ L_{11} & {L_{12} + L_{21} \over 2} & {L_{13} + L_{31} \over 2} \\ \\ {L_{21} + L_{12} \over 2} & L_{22} & {L_{23} + L_{32} \over 2} \\ \\ {L_{31} + L_{13} \over 2} & {L_{32} + L_{23} \over 2} & L_{33} } \right] \]
The components of the spin tensor, \({\bf W}\), are
\[ {\bf W} = \left[ \matrix{ 0 & {L_{12} - L_{21} \over 2} & {L_{13} - L_{31} \over 2} \\ \\ {L_{21} - L_{12} \over 2} & 0 & {L_{23} - L_{32} \over 2} \\ \\ {L_{31} - L_{13} \over 2} & {L_{32} - L_{23} \over 2} & 0 } \right] \]
In terms of partials, the rate of deformation tensor is
\[ {\bf D} = \left[ \matrix{ {\partial v_x \over \partial x} & {1 \over 2} \left( {\partial v_x \over \partial y} + {\partial v_y \over \partial x} \right) & {1 \over 2} \left( {\partial v_x \over \partial z} + {\partial v_z \over \partial x} \right) \\ \\ {1 \over 2} \left( {\partial v_y \over \partial x} + {\partial v_x \over \partial y} \right) & {\partial v_y \over \partial y} & {1 \over 2} \left( {\partial v_y \over \partial z} + {\partial v_z \over \partial y} \right) \\ \\ {1 \over 2} \left( {\partial v_z \over \partial x} + {\partial v_x \over \partial z} \right) & {1 \over 2} \left( {\partial v_z \over \partial y} + {\partial v_y \over \partial z} \right) & {\partial v_z \over \partial z} } \right] \]
and the spin tensor is
\[ {\bf W} = \left[ \matrix{ 0 & {1 \over 2} \left( {\partial v_x \over \partial y} - {\partial v_y \over \partial x} \right) & {1 \over 2} \left( {\partial v_x \over \partial z} - {\partial v_z \over \partial x} \right) \\ \\ {1 \over 2} \left( {\partial v_y \over \partial x} - {\partial v_x \over \partial y} \right) & 0 & {1 \over 2} \left( {\partial v_y \over \partial z} - {\partial v_z \over \partial y} \right) \\ \\ {1 \over 2} \left( {\partial v_z \over \partial x} - {\partial v_x \over \partial z} \right) & {1 \over 2} \left( {\partial v_z \over \partial y} - {\partial v_y \over \partial z} \right) & 0 } \right] \]
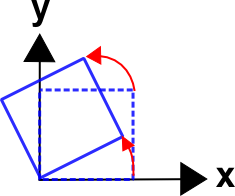
Spin Tensor and Angular Velocity Vector
Consider the object in the figure rotating counter-clockwise about the \(z\) axis at an angular velocity, \(\omega_z\). Calculate the \(W_{21}\) component of the spin tensor.The following equations describe the rotation.
\[ \begin{eqnarray} x & = & X \cos \omega_z t & - & Y \sin \omega_z t \\ y & = & X \sin \omega_z t & + & Y \cos \omega_z t \end{eqnarray} \]
Take the time derivative of the equations to obtain \(v_x\) and \(v_y\).
\[ \begin{eqnarray} v_x & = & - \omega_z X \sin \omega_z t & - & \omega_z Y \cos \omega_z t \\ v_y & = & \;\;\,\omega_z X \cos \omega_z t & - & \omega_z Y \sin \omega_z t \end{eqnarray} \]
This gives us \(v_x\) and \(v_y\) in terms of \(X\) and \(Y\). But we need \(v_x\) and \(v_y\) in terms of \(x\) and \(y\) instead, in order to compute the spin tensor components. This can be accomplished by first inverting the first pair of equations to obtain \(X\) and \(Y\) in terms of \(x\) and \(y\), and substituting these into the second pair of equations.
Inverting the first equations gives
\[ \begin{eqnarray} X & = & \;\;\,x \cos \omega_z t & + & y \sin \omega_z t \\ Y & = & -x \sin \omega_z t & + & y \cos \omega_z t \end{eqnarray} \]
(Note that this amounts to starting with \({\bf x} = {\bf R} \cdot {\bf X}\) and inverting it to obtain \({\bf X} = {\bf R^{-1}} \cdot {\bf x}\))
Substituting these inverted equations into the second pair containing the velocity components gives a remarkably simple result.
\[ \begin{eqnarray} v_x & = & - \omega_z \, y \\ v_y & = & \;\;\,\omega_z \, x \end{eqnarray} \]
It is now possible to easily calculate the \(W_{21}\) component of the spin tensor.
\[ \begin{eqnarray} W_{21} \quad = \quad {1 \over 2} \left( {\partial v_y \over \partial x} - {\partial v_x \over \partial y} \right) \quad = \quad {1 \over 2} \left( {\partial (\omega_z \, x) \over \partial x} - {\partial (-\omega_z \, y) \over \partial y} \right) \quad = \quad \omega_z \end{eqnarray} \]
This simple 2-D example demonstrates how a spin tensor can contain components of the angular velocity vector.
\[ {\bf W} = \left[ \matrix{ \;\;0 & -\omega_z & \;\;\;\omega_y \\ \;\;\;\omega_z & \;\;0 & -\omega_x \\ -\omega_y & \;\;\;\omega_x & \;\;0 } \right] \]
where \(\boldsymbol{\omega}\) is the angular velocity vector. It is directly related to rotation about an axis discussed on the rotation matrix page. Recall that it contained a rotation angle, \(\alpha\), about an axis, \({\bf p} = (p_x, p_y, p_z)\). The relationship is
\[ \omega_x \, = \, \dot \alpha \, p_x = {1 \over 2} \left( {\partial v_z \over \partial y} - {\partial v_y \over \partial z} \right) \qquad \qquad \omega_y \, = \, \dot \alpha \, p_y = {1 \over 2} \left( {\partial v_x \over \partial z} - {\partial v_z \over \partial x} \right) \]
\[ \omega_z \, = \, \dot \alpha \, p_z = {1 \over 2} \left( {\partial v_y \over \partial x} - {\partial v_x \over \partial y} \right) \]
Rate of Deformation and Spin Example
If the velocity gradient is\[ {\bf L} = \left[ \matrix{ \;\;\;0.5 & \;\;\;0.4 & \;\;\;0.3 \\ \;\;\;0.2 & -0.1 & -0.2 \\ -0.3 & \;\;\;0.4 & -0.1 } \right] \]
Then the rate of deformation tensor is
and the spin tensor is
\[ {\bf W} = \left[ \matrix{ \;\;\;0.0 & \;\;0.1 & \;\;\;0.3 \\ -0.1 & \;\;0.0 & -0.3 \\ -0.3 & \;\;0.3 & \;\;\;0.0 } \right] \]
Rate of Deformation and True Strain
The next webpage on true strains will go into this topic in more depth, but for completeness, it will be quickly summarized here.The normal components of the rate of deformation tensor also give the time rates of change of true strain. The relationships are as follows.
\[ D_{11} = \dot \epsilon^\text{True}_1 = {d \over dt} \ln \left( {L_F \over L_o} \right) \]
Also,
\[ D_{11} + D_{22} + D_{33} = \dot \epsilon^\text{True}_{\text{Vol}} \]
And this applies regardless of the strain level or orientation.
Velocity Gradients and the Polar Decomposition
Merging the polar decomposition together with the velocity gradient gives some very interesting results. Start with\[ {\bf F} = {\bf R} \cdot {\bf U} \]
The time derivative is
\[ \dot {\bf F} = {\bf R} \cdot \dot {\bf U} + \dot {\bf R} \cdot {\bf U} \]
The inverse of \({\bf F}\) is
\[ {\bf F}^{-1} = {\bf U}^{-1} \! \cdot {\bf R}^{-1} \]
So \(\dot {\bf F} \cdot {\bf F}^{-1}\) is
\[ \begin{eqnarray} {\bf L} = \dot {\bf F} \cdot {\bf F}^{-1} & = & ( {\bf R} \cdot \dot {\bf U} + \dot {\bf R} \cdot {\bf U} ) ( {\bf U}^{-1} \! \cdot {\bf R}^{-1} ) \\ \\ & = & {\bf R} \cdot \dot {\bf U} \cdot {\bf U}^{-1} \! \cdot {\bf R}^{-1} + \dot {\bf R} \cdot {\bf U} \cdot {\bf U}^{-1} \! \cdot {\bf R}^{-1} \\ \end{eqnarray} \]
But \({\bf U} \cdot {\bf U}^{-1}\) cancels out, leaving
\[ \begin{eqnarray} {\bf L} = \dot {\bf F} \cdot {\bf F}^{-1} & = & {\bf R} \cdot ( \dot {\bf U} \cdot {\bf U}^{-1} ) \cdot {\bf R}^{-1} + \dot {\bf R} \cdot {\bf R}^{-1} \\ \end{eqnarray} \]
And \({\bf R}^{-1} = {\bf R}^T\), so finally
\[ {\bf L} \, = \, {\bf R} \cdot ( \dot {\bf U} \cdot {\bf U}^{-1} ) \cdot {\bf R}^T + \dot {\bf R} \cdot {\bf R}^T \\ \]
The result is interesting because of how \({\bf L}\) has become partitioned into two contributing terms. The first term, \({\bf R} \cdot ( \dot {\bf U} \cdot {\bf U}^{-1} ) \cdot {\bf R}^T\), gives the contribution due solely to deformations. This is evident because if there is no deformation, then \(\dot {\bf U}\) is zero, and the entire first term is zero as well.
If deformations are taking place, then the first term can have both symmetric and antisymmetric contributions to \({\bf L}\). The antisymmetric (spin) contribution could come from simple shear, for example, \(D/T\) style. Note that since \({\bf U}\) is always related to the reference coordinate system, like Green strain for example, it is multiplied by \({\bf R}\) and \({\bf R}^T\) to rotate it to the current orientation just like
\[ {\bf V} = {\bf R} \cdot {\bf U} \cdot {\bf R}^T \]
Note the similarity!
The second term, \(\dot {\bf R} \cdot {\bf R}^T\), is just as interesting. Suppose there is only rigid body rotation taking place. Then \(\dot {\bf U} = 0\) and only \(\dot {\bf R} \cdot {\bf R}^T\) is left to contribute to \({\bf L}\). But this must be entirely "spin" because there is no deformation taking place. So \(\dot {\bf R} \cdot {\bf R}^T\) produces an antisymmetric result, which can easily be re-interpreted into \(\boldsymbol{\omega} = (\omega_x, \omega_y, \omega_z)\).
2-D Rigid Body Rotation Example
Start with a 2-D rotation matrix, \({\bf R}\), and calculate \(\dot {\bf R} \cdot {\bf R}^T\).\[ {\bf R} = \left[ \matrix{ \cos \theta & -\sin \theta \\ \sin \theta & \;\;\;\cos \theta } \right] \]
so \(\dot {\bf R}\) is
\[ \dot {\bf R} = \omega \left[ \matrix{ -\sin \theta & -\cos \theta \\ \;\;\;\cos \theta & -\sin \theta } \right] \]
And \({\bf R}^T\) is
\[ {\bf R}^T = \left[ \matrix{ \;\;\;\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta } \right] \]
So multiplying the two together gives
\[ \begin{eqnarray} \dot {\bf R} \cdot {\bf R}^T & = & \omega \left[ \matrix{ -\sin \theta & -\cos \theta \\ \;\;\;\cos \theta & -\sin \theta } \right] \left[ \matrix{ \;\;\;\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta } \right] \\ \\ \\ & = & \omega \left[ \matrix{ 0 & -1 \\ 1 & \;\;\;0 } \right] \end{eqnarray} \]
So the result is indeed an antisymmetric spin tensor.
Velocity Gradient and Green Strain
The last relationship to develop is between the velocity gradient and the time derivative of the Green strain tensor. Start with the definition of Green strain.\[ {\bf E} = {1 \over 2} \left[ {\bf F}^T \cdot {\bf F} - {\bf I} \right] \]
Take the derivative of \({\bf E}\) to get
\[ \dot {\bf E} = {1 \over 2} \left[ {\bf F}^T \cdot \dot {\bf F} + \dot {\bf F}^T \cdot {\bf F} \right] \]
Now insert \({\bf L}\cdot{\bf F}\) for \(\dot {\bf F}\) and \({\bf F}^T\cdot{\bf L}^T\) for \(\dot {\bf F}^T\).
\[ \dot {\bf E} = {1 \over 2} \left[ {\bf F}^T \cdot {\bf L} \cdot {\bf F} + {\bf F}^T \cdot {\bf L}^T \cdot {\bf F} \right] \]
Next, notice that each term begins with \({\bf F}^T\) and ends with \({\bf F}\). So things can be regrouped as follows.
\[ \dot {\bf E} = {\bf F}^T \cdot \left( { {\bf L} + {\bf L}^T \over 2} \right) \cdot {\bf F} \]
\[ \dot {\bf E} = {\bf F}^T \cdot {\bf D} \cdot {\bf F} \]
And it can be inverted to give
\[ {\bf D} = {\bf F}^{-T} \cdot \dot {\bf E} \cdot {\bf F}^{-1} \]
These equations relating \(\dot {\bf E}\) and \({\bf D}\) will be used to identify pairs of energetically conjugate stress and strain tensors.