Introduction
This page will tackle the influence of rubber properties on certain aspects of tire performance. In particular, the impact of rubber modulus and phase lag on a tire's heat generation, operating temperature(s), rolling resistance, and traction performance will be discussed.Background
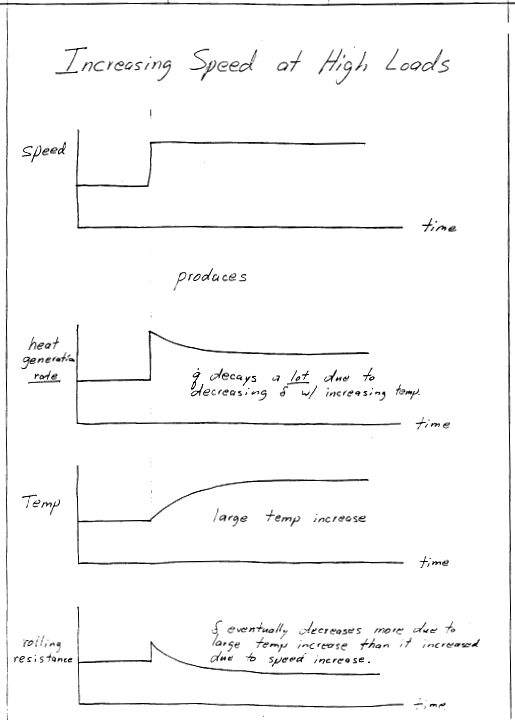
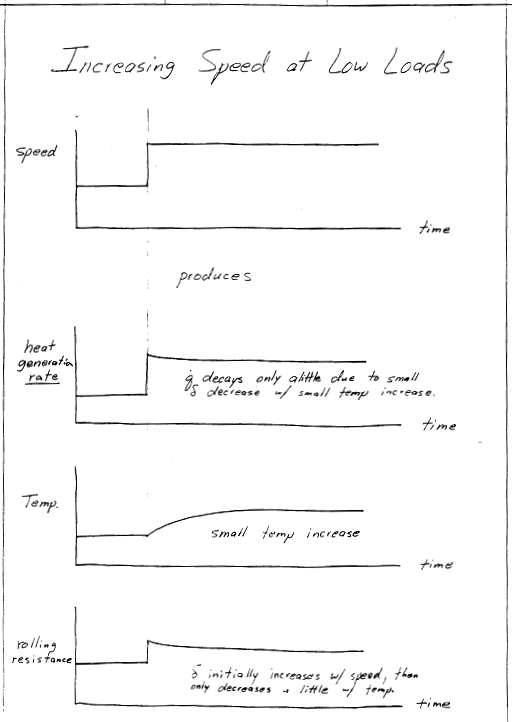
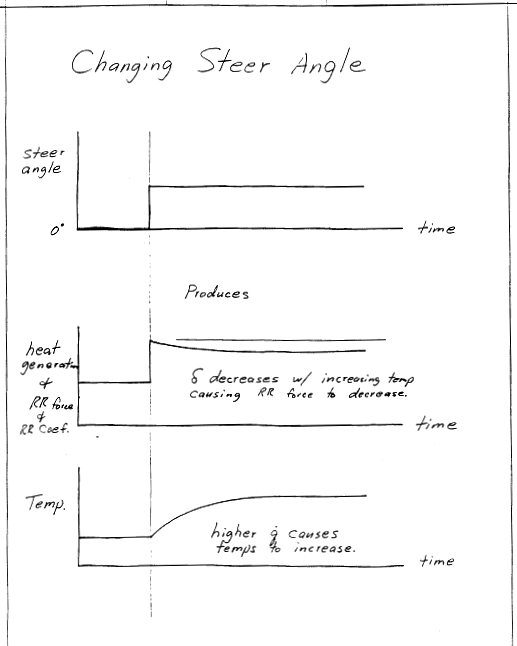
The key to many aspects of tire performance is the rate of heat generation as it rolls due to hysteretic damping present in the rubber compounds. Hysteretic damping results in a phase lag between the stress and strain cycles, as shown in the sketch.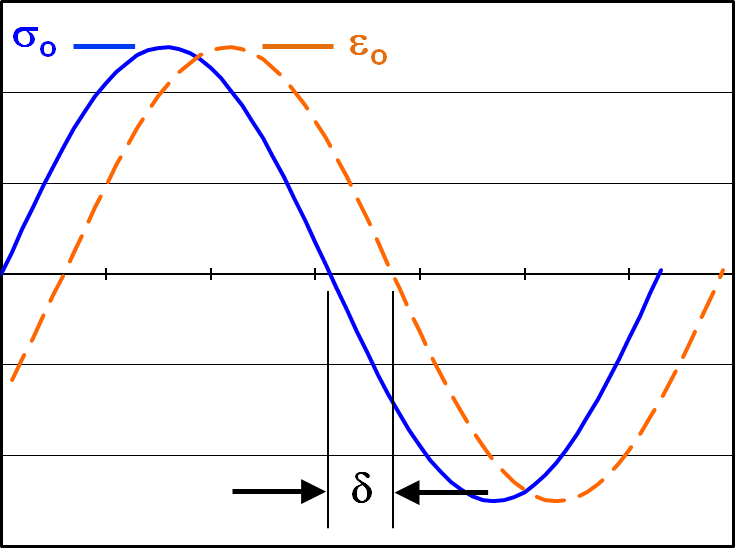
The transient stress and strain signals are described by
\[ \sigma_{(t)} = \sigma_o \sin (\omega t) \qquad \text{and} \qquad \epsilon_{(t)} = \epsilon_o \sin (\omega t - \delta) \]
They are substituted into the following equation to compute the heat generation per cycle
\[ W = \int \sigma_{(t)} d \epsilon_{(t)} \]
which results in
\[ W = \pi \, \sigma_o \, \epsilon_o \sin(\delta) \]
This represents the mechanical energy loss per cycle, which would also be "per tire rotation" The mechanical energy lost must equal the heat generated in order to satisfy the 1st Law: \(W_\text{lost} = Q_\text{generated}\). And multiplying this by the tire's rotational frequency, \(f\), gives the heat generation rate, \(\dot Q\).
\[ \dot Q = f \, \pi \, \sigma_o \, \epsilon_o \sin(\delta) \]
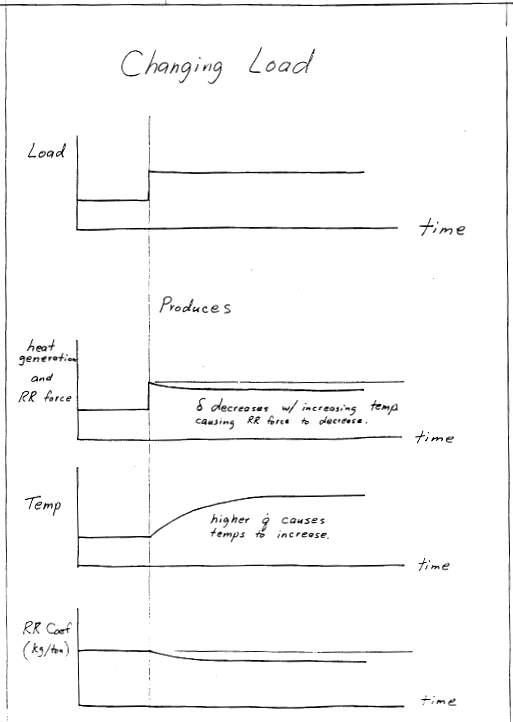
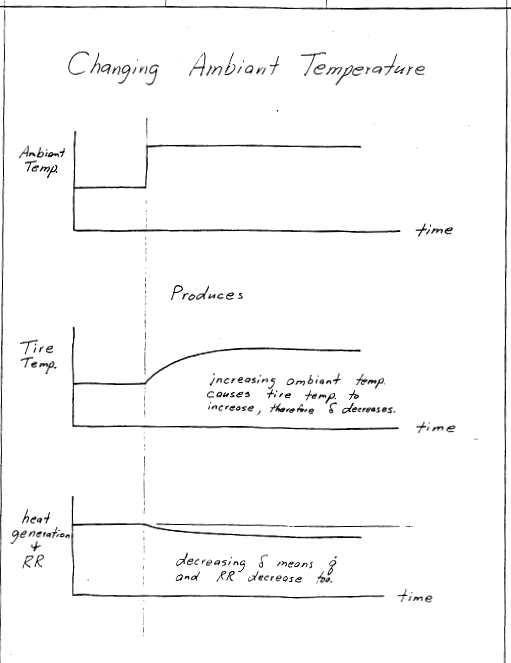
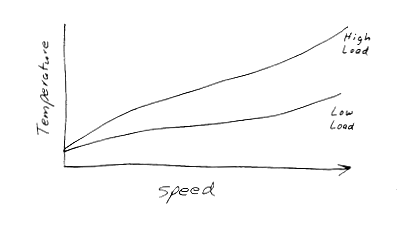
Of course, this is simplified. In the real tire, 3-D deformations take place, and the deformation histories are not simple sinusoids. But the trends here are correct. Heat generation rate increases with (i) the tire's rotational frequency, \(f\), (ii) the material's phase lag, \(\delta\), and (iii) the product of the stress and strain cycle amplitudes \(\sigma_o \epsilon_o\).
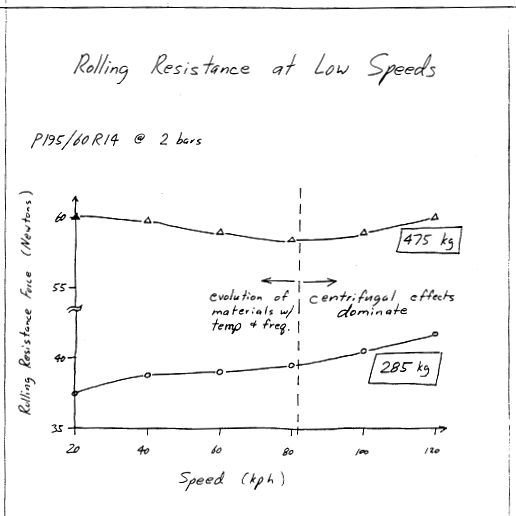
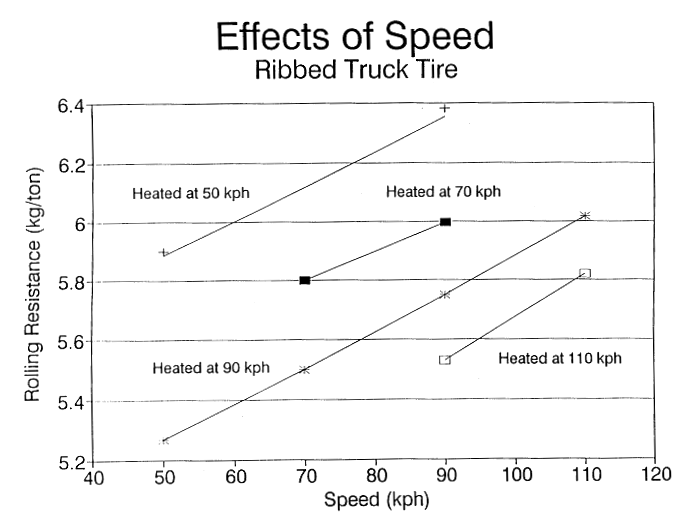
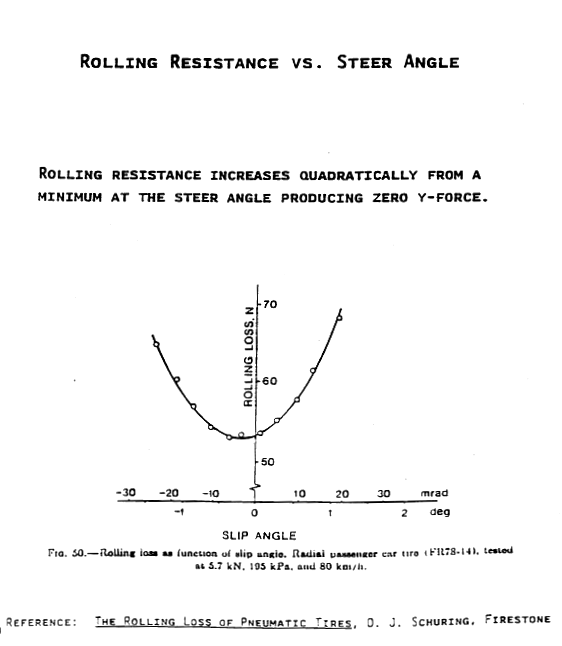
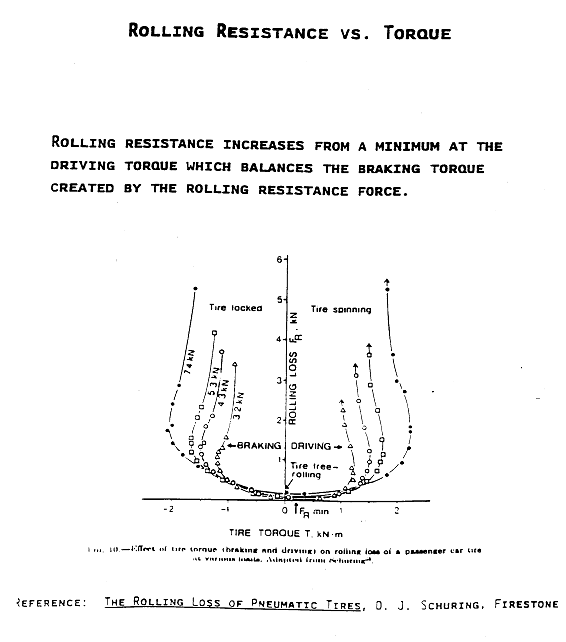
Rolling Resistance Force * Speed = Heat Generation Rate